Předpoklady Nesplněny
Přirozená čísla a zákony o operacíchČíselné obory a základní znalosti
-%
Celá čísla
Řešená cvičení
Komutativita a asociativita
Základní škola • 2 min
Určete, jestli je odčítání komutativní a asociativní.
Hledání dvojic
Základní škola • 2 min
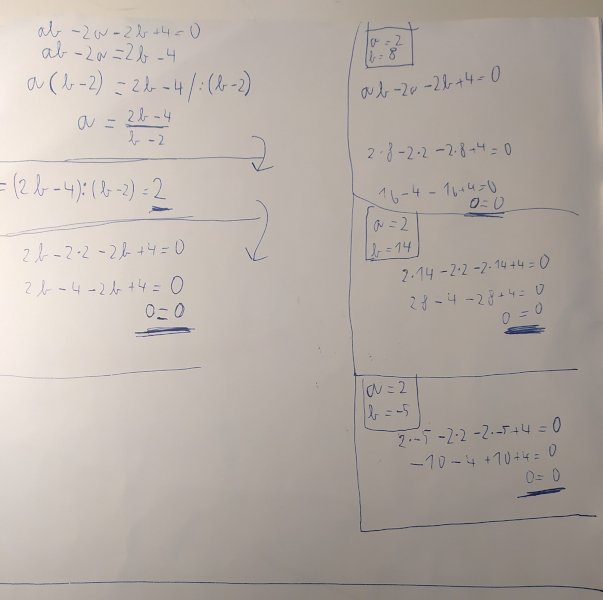
Nalezněte všechny dvojice celých čísel \(a\), \(b\), pro která platí:
\(ab-2a-2b+4=0\)
Hledání dvojic
Základní škola • 8 min
Nalezněte všechny dvojice celých čísel \(a\), \(b\), pro která platí:
\(a^2-5=4b^2\)
Testy
-%
Základy pro celá čísla
Základní škola • 5 min
-%
Celá čísla -%
Opačné číslo -%
Uzavřenost operací -%
Označení -%
Neutrální operace -%
Podrobnosti o látce
Klíčová slova
Číselný obor Celá čísla Opačné číslo Neutrální prvek UzavřenostAutor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Základní škola
Odhadovaná délka studia
0 h 36 min
Poznámka k videu
Obor celých čísel označujeme jako \(\mathbb{Z}\). Celá čísla "napravují" přirozená čísla o uzavřenost operace rozdílu (odčítání). To znamená, že celá čísla jsou uzavřená na operaci sčítání, násobení a odčítání, stále ovšem nejsou uzavřená a operaci dělení (mohli bychom využít stejný protipříklad, jako v předchozích odstavcích).
Obor celých čísel je první, ve kterém má smysl hovořit o opačného prvku. Ten vždy vždy určujeme k nějakému konkrétnímu číslu. Je to takové číslo, které v součtu s původním číslem dává nulu. Například pro číslo \(-3\) je opačné číslo \(3\), jelikož \(-3+3=0\).
Stejně tak je dobré zmínit pojem neutrálního prvku ke sčítání a k násobení. Neutrální prvek je číslo, které při provedení dané operace s jakýmkoli číslem toto číslo nemění. Pro sčítání je to \(0\) a pro násobení je to \(1\).
Poznámka pro zvídavé:
Obecně máme mnohem více druhů operací, ať už jsou to binární (ze dvou čísel vytváříme jedno nové, například sčítání, odčítání, násobení nebo dělení) nebo unární (z jednoho čísla tvoříme jedno nové, například umocňování, odmocňování nebo absolutní hodnota). O tom ale více v tématu Abstraktní algebra, stejně jako o vlastnostech operací, jako jsou komutativita, asociativita či neutrální prvek.
Stejně tak by někoho mohlo zarazit, jestli existují situace, kdy (pro nás naprosto přirozený) zákon komutativity neplatí. A je tomu skutečně tak, takové situace existují, je to například v případě součinu matic nebo skládání permutací, ale o tom v budoucnu :)
Komentáře
Drakonatus 08. 03. 2021 • 08:48
U druhého řešeného příkladu vám vyšlo že jediné možné řešení jsou reálná čísla (2;2). Příklad jsem počítal trochu jinou metodou a vyšlo mi, že výsledkem mohou být čísla dva a jakékoliv reálné číslo, zkoušel jsem různé kombinace čísel dva a libovolného reálného i jako zkoušku a rovnice vždy vyšla, takže teď fakt nevím, jak to je.
Dominik Chládek 08. 03. 2021 • 11:10
Dobrý den,
moc děkuji za poznámku, ve skutečnosti je to tak, že řešením můžou být dvojice čísel takové, že stačí když jendo z těch čísel je dvojka, tedy v podtstatě jsou možné i dvojice \(a=100\), \(b=2\) a podobně. Součin je roven nule, pokud se jeden z těch členů rovná nule, takže to je určitě chyba na mojí straně, moc se omlouvám za zmatení a děkuji za upozornění!