Obecný a existenční kvantifikátor
Řešená cvičení
Kvantifikace výroku a pravdivost
Střední škola • 3 min
Přepište pomocí kvantifikátorů věty a určete jejich pravdivost:
1) Druhá mocnina každého reálného čísla je nezáporná.
2) Existuje přirozené číslo, které je kořenem rovnice \(x^2-16=0\).
Kvantifikace výroku a pravdivost
Střední škola • 7 min
Kvantifikujte výrazy na výroky a určete pravdivost:
1) \(x+1=2\)
2) \(|x| \geq 1\)
Kvantifikace výroku a pravdivost
Střední škola • 5 min
Přepište následující výrazy slovně a určete jejich pravdivost:
1) \(\left(\forall x\in\mathbb{R}\right)\left(\sqrt{x^2}=\left|x\right|\right)\)
2) \(\left(\exists x\in\mathbb{Z}\right)\left(\left(x+3\right)^2<1\right)\)
Testy
-%
Obecný a existenční kvantifikátor
Střední škola • 5 min
-%
Existenční kvantifikátor -%
Obecný kvantifikátor -%
Pravdivý výrok -%
Pravdivý výrok -%
Pravdivý výrok -%
Kvantifikace výrazů
Střední škola • 7 min
-%
Příklad -%
Příklad -%
Slovní kvantifikace
Střední škola • 7 min
-%
Kvantifikace -%
Kvantifikace -%
Podrobnosti o látce
Výpisky ke stažení
Klíčová slova
Výrok Kvantifikátor Obecný kvantifikátor Existenční kvantifikátorAutor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 43 min
Komentáře
Jan Míka upraveno: 17. 02. 2025 • 22:59
Dobrý den. Když je druhá mocnina reálného čísla x a zároveň jeho druhá odmocnina, tak se nejdříve dané číslo musí umocnit a teprve potom odmocnit? Z Vašich materiálů na odmocniny a lomené výrazy si pamatuji, že nezáleží, jestli se nejdříve umocní a pak odmocní nebo se to provede naopak. Vizte přílohu:
Děkuji
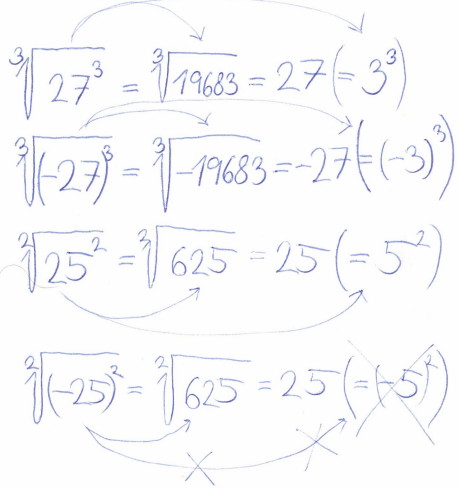
Jan Míka 18. 02. 2025 • 13:43
Mockrát děkuji :)
Dominik Chládek 18. 02. 2025 • 09:56
Dobrý den, nezáleží na tom pořadí, pokud máte uvnitř nezáporné číslo (tedy číslo, větší nebo rovno nule). Pokud máte uvnitř záporné číslo, tak na pořadí naopak záleží a to hodně, jelikož v některých situacích se jedná o definovaný výraz a v jiných se jedná o nedefinovaný výraz, jakou jsou dva Vaše poslední příklady :)
Ketiv 16. 03. 2018 • 12:16
Jsem hlupák :D mockrát děkuji :)
Dominik Chládek 16. 03. 2018 • 12:02
Dobrý den,
tak se zkusme zamyslet, patří nula do racionálních čísel? Racionální čísla jsou všechna čísla, která se dají zapsat ve tvaru zlomku. Dá se tedy napsat nula ve tvaru zlomku? Dá, tak například:
\(\dfrac01;\dfrac09;-\dfrac05\)
a podobně. Takže nula patří do racionálních čísel :)
Ketiv 16. 03. 2018 • 10:41
Dobrý den, mám dotaz k otázce číslo 4. (∃x∈ _ ):(|x|≤0), jako správné odpovědi jsou uvedeny množiny celých čísel, realných čísel a racionálních čísel. Celé a realné mi dávají smysl, protože obsahují 0. Proto chápu (∃x∈ Z ):(|0|≤0) a také (∃x∈ R ):(|0|≤0). Ale nejsem si jistý zda-li nějaké jiné číslo než 0 splní tuto podmínku. A také zda racionální čísla obsahují 0, což jsem si myslel, že neobsahují. Chtěl bych Vás poprosit o objasnění této otázky. Děkuji