Předpoklady Nesplněny
Absolutní hodnotaČíselné obory a základní znalosti
-%
Výroková logika
-%
Výroková logika
-%
Definice vlastní limity
Řešená cvičení
Velikost člene
Střední škola • 3 min
Od kterého členu má posloupnost:
\(\left(\dfrac1{2n+3}\right)_{n=1}^\infty\)
všechny členy menší než:
\(1)\;\dfrac1{10}\\ 2)\;\dfrac1{100}\\ 3)\;\dfrac1{1000}\)
Testy
-%
Definice vlastní limity
Střední škola • 2 min
-%
Definice -%
Vlastní limita -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 24 min
Komentáře
Barbora 27. 10. 2023 • 21:46
Můžu se zeptat, jak vypočítat druhou část tohoto příkladu? Limitu vypočítám, ale nejsem si jistá tím, jak se dopracuju k výsledku, pro která n se hodnoty členů liší od A o méně než ε.
Jinak videa super 👌
Dominik Chládek 13. 11. 2023 • 10:02
Teď musíte použít definici limity posloupnosti, tedy rozepsat tu nerovnost která řká, že:
\(|a_n-\frac13|<\frac1{100}\)
Barbora 12. 11. 2023 • 22:17
Mám jen tu limitu a ta mi vyšla jako 1/3 🙈
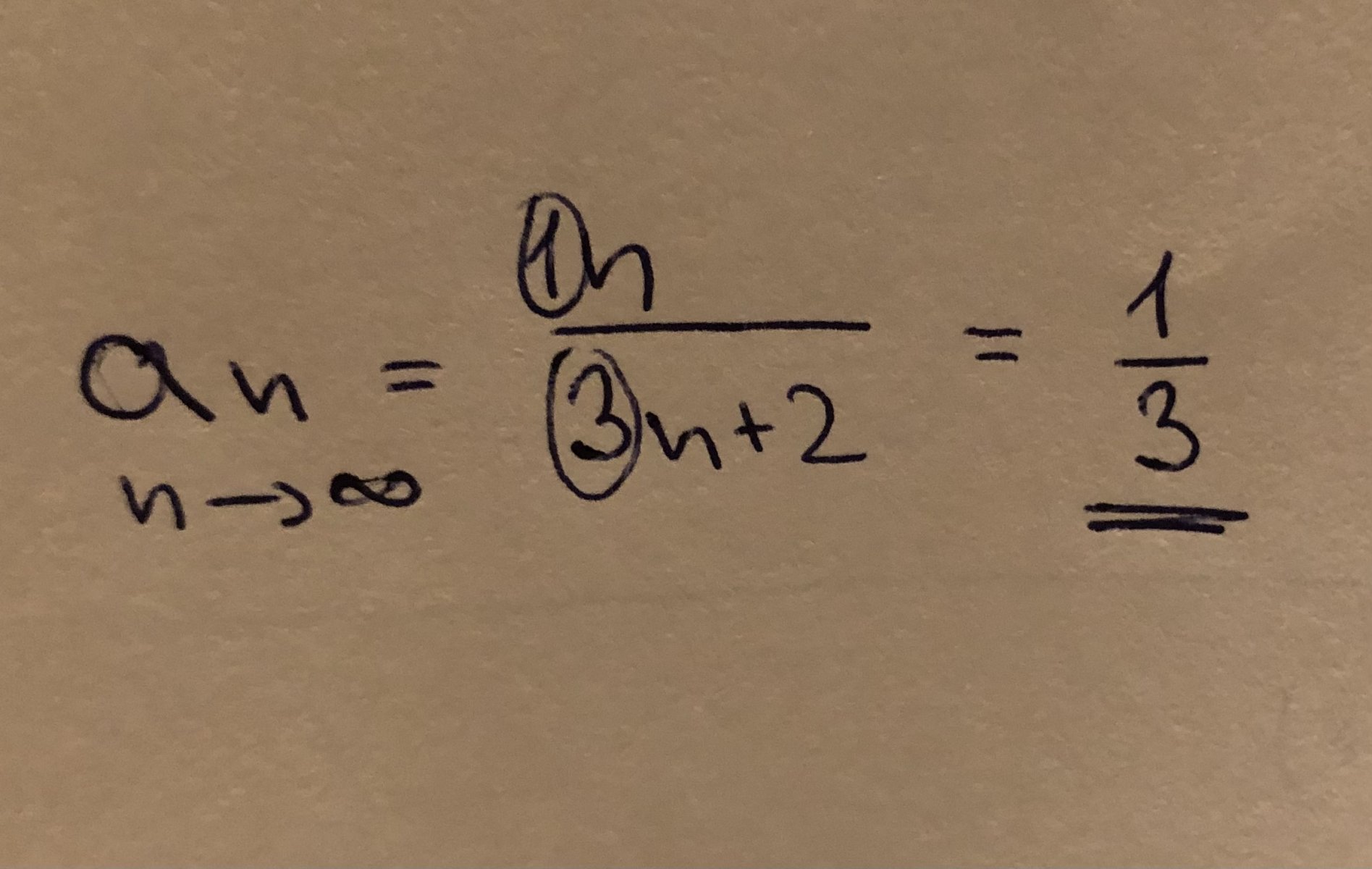
Dominik Chládek 30. 10. 2023 • 11:31
Dobrý den, a můžete nahrát kam až jste se dostala? :)
Daniel 27. 08. 2020 • 20:46
Konečně mám pocit, že tomu trochu začínám rozumět. Když člověk ví, jak na to, tak to ani není moc složité.
Dominik Chládek 27. 08. 2020 • 23:27
To mám obrovskou radost a moc držím palce! :)
Dominik Chládek 22. 06. 2017 • 22:19
Díky moc za pochvalu! :)
veruunek 21. 06. 2017 • 23:41
Děkuji za skvělé vysvětlení :-)