Předpoklady Nesplněny
Speciální podílové limityPosloupnosti a nekonečné řady
-%
Limita a spojitost funkce
-%
Speciální typ podílu
V čase 12:16 je chyba ve znaménku na konci, výpočet má být:
\(\underset{x\rightarrow-\infty}{lim}\dfrac{2x^4-3x+5}{1-x^3}=\underset{x\rightarrow-\infty}{lim}\dfrac{2x-{\displaystyle\frac3{x^2}}+{\displaystyle\frac5{x^3}}}{{\displaystyle\frac1{x^3}}-1}=\\=\dfrac{-2\infty-0+0}{0-1}=+\infty\)
Omlouvám se za chybu :)
Řešená cvičení
Limita s exponenciálou
Vysoká škola • 1 min
Vypočítejte:
\(\displaystyle \underset{x\rightarrow-\infty}{\lim}e^\frac{x^3+9x^2-2}{x^2+3}\)
Limita s polynomem
Vysoká škola • 7 min
Vypočítejte:
\(1)\;\displaystyle \underset{x\rightarrow+\infty}{\lim}\left(\frac{3x^4-6x^3+1}{6x^4-12x+31}\right)\\2)\;\displaystyle \underset{x\rightarrow-\infty}{\lim}\left(\frac{x^4+4x^2-1}{x+2}\right)\)
Limita s polynomem
Vysoká škola • 5 min
Vypočítejte:
\(1)\;\displaystyle \underset{x\rightarrow-\infty}{\lim}\left(\frac{x^2-3x+4}{x-6x^3+2}\right)\\2)\;\displaystyle \underset{x\rightarrow+\infty}{\lim}\left(\frac{3-\pi x^3+26x}{2x+6x^2-2}\right)\)
Testy
-%
Speciální typ podílu
Střední škola • 4 min
-%
Definice -%
Počítání -%
Počítání -%
Počítání -%
Podílové limity
Vysoká škola • 10 min
-%
Zlomek -%
Zlomek -%
Zlomek -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
1 h 1 min
Komentáře
Jirka Stránský 16. 01. 2026 • 06:42
Ahoj Dominiku, super video a zase se prokousávám. Ta finta na to rychlé určení ve videu je fajn, jen je škoda, že si k tomuto skvělému videu neudělal pdf soubor právě s tou chytrou teorií o tom co bude výsledkem podle toho kde je jaká mocnina, jako tabulkou :-) Nebo je někde v jiné kapitole?
Dominik Chládek 16. 01. 2026 • 12:07
Ahooj, díky za inspiraci, nikde to v PDF není, ale pokusím se to dodat! :)
Klára 17. 12. 2023 • 17:17
Dobrý den, nejprve moc díky za vaše videa! Jsou skvělá!
Mám jeden příklad, který mi výpočtem i ve výsledcích v cvičebnici vyjde 1. Pokud bych uplatnila pravidlo, že pokud má čitatel vyšší mocninu, vyjde +- ∞ , tak netuším, kde dělám chybu. Díky moc.
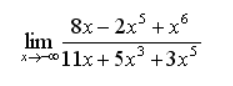
Klára 19. 12. 2023 • 20:03
Moc díky za odpověď!
Dominik Chládek 19. 12. 2023 • 18:14
Dobrý den, vyjde to určitě - nekonečno, jedna ne, takže to mají špatně ve sbírce :)
Dominik 06. 09. 2023 • 14:04
Zdravím, je nutné po každé úpravě psát limitu z nově upraveného výrazu, a nebo stačí napsat = bez limity? Snad jsem to napsal aspoň trochu srozumitelně, kdyžtak bych poslal foto, jak to myslím.
Děkuji :)
Dominik 06. 09. 2023 • 14:04
Zdravím, je nutné po každé úpravě psát limitu z nově upraveného výrazu, a nebo stačí napsat = bez limity? Snad jsem to napsal aspoň trochu srozumitelně, kdyžtak bych poslal foto, jak to myslím.
Děkuji :)
Rostislav Fibich 23. 07. 2022 • 14:39
Dobrý den, rád bych se zeptal na druhý příklad pod názvem limita s polynomem, kde výsledkem má být -∞. K tomuto výsledku jste došel po vytkuntí X^3, následně zbylo x^3 + 4*∞/1, což je tedy -∞. Pokud bych ale vytknul X^2, měl bych po upravení v čitateli x^2*(X^2 +4 -1/X^2) a ve jmenovateli X^2*(1/x + 2/x^2). Následně by to bylo x^2 +4 / 1, po dosazení (-∞)^2 + 4/1, což mi vyjde jako +∞. Děkuji za Vaši odpověď.
Dominik Chládek 25. 07. 2022 • 10:14
Dobrý den, ve jmenovaeli byste měl 0*nekonečno a to je neurčitý výraz :)
Michi 14. 04. 2021 • 11:21
Zdravím, mám otázku, pri poslednom riešenom príklade vyšlo nekonečno krát PÍ štvrtin, čo je menšie ako 1 keďže PÍ je 3.14.... a teda limita by mala ísť k nule nie k nekonečnu ak sa nemýlim
Dominik Chládek 15. 04. 2021 • 23:19
Není za co, moc děkuji za pochvalu :) priorita je aby to pomáhalo co nejvíce lidem, proto je většina zadarmo :)
Michi 15. 04. 2021 • 21:06
ďakujem za odpoveď, pomýlil som si to s exponenciálou, ináč super práca, mohol by si všetok obsah spoplatniť alebo ak to chceš nechať zadarmo tak aspoň spraviť dobrú reklamu na všetkých sociálnych sieťach aby si to viacej ľudí predplatilo
Dominik Chládek 15. 04. 2021 • 09:51
Dobrý den,
myslíte u toho příkladu s arcustangens? :) tak máte nekonečno krát kladné číslo, tedy nekonečno. Vy se to zřejmě pletete s exponenciálou, která pro základ menší než jedna jde k nule, ale to není tento případ :)
Dominik Chládek 17. 08. 2018 • 08:19
Dobrý den, určitě máte pravdu, ale jde mi o to že jsem vedle uváděl výpočty a na základě nich jsem vše poté počítal z hlavy. A v tom konkrétním případě na který se ptáte mám dole vyšší mocninu než nahoře, takže po vytknutí a pokrácení by mi zůstala jenom mocnina dole a vše by šlo k nule :)
JirkaK 16. 08. 2018 • 22:46
Dobrý den, u příkladu v čase 10:42 jste na základě mocnin napsal výsledek 0. Pokud bychom ale dosadili, získali bychom nekonečno/nekonečno a to přeci není definováno. Doufám, že se nepletu. Jinak mockrát děkuji, Jirka.
Dominik Chládek 27. 10. 2017 • 21:48
Dobrý den, to je zrychlený proces krácení, když tam přímo dosadíte tak Vám to nevyjde. To budete mít vždy neurčitý výraz...
lenjan 27. 10. 2017 • 18:11
Zdravím. Nerozumiem prečo v poslednom príklade je v menovateli 2∞/-1 keď v príklade je -(x^3). Tomu 2∞ chápem to to -1 mi nedáva zmysel. Ja som si myslel že aj tam môžem doplniť - (-∞^3) čo ale logicky potom výnde 2∞/ - (-∞^3) a v tom prípade by to bol neurčitý výraz.