Předchozí látkaPředpoklady Nesplněny
Vzorce pro goniometrické funkceGoniometrie a trigonometrie
-%
Limita a spojitost funkce
-%
Výpočet limity se vzorci
Řešená cvičení
Limita s exponentem a polynomem
Vysoká škola • 4 min
Vypočítejte:
\(\displaystyle \underset{x\rightarrow+\infty}{\lim}\left(1+\frac1{x^2}\right)^x\)
Limita s exponentem a polynomem
Vysoká škola • 6 min
Vypočítejte:
\(\displaystyle \underset{x\rightarrow+\infty}{\lim}\left(\frac{2x+5}{2x+3}\right)^{x+1}\)
Limita s exponentem a polynomem
Vysoká škola • 1 min
Vypočítejte:
\(\displaystyle \underset{x\rightarrow1}{\lim}\left(\frac{x-1}{x^2-1}\right)^{x+1}\)
Testy
-%
Výpočet limity se vzorci
Střední škola • 3 min
-%
Počítání -%
Počítání -%
Vzorce v limitách
Vysoká škola • 10 min
-%
Sinus -%
Sinus -%
Mocnina -%
Mocnina -%
Podrobnosti o látce
Výpisky ke stažení
Výpočet limity se vzorci
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
1 h 18 min
Komentáře
Barbora Štechová upraveno: 22. 04. 2024 • 14:25
Dobrý den, chtěla bych se zeptat, zda by šel 2.příklad vypočítat stejně jako první - a tedy, že rozepíšeme limitu jako
lim(sin5x/3x) = lim(sinx/x) * (5/3) = lim (1 * 5/3) = 5/3?
Předem děkuji za odpověď!
Dominik Chládek 22. 04. 2024 • 22:35
Dobrý den, bohužel ne, nemáte jak vytknout tu pětku v sin(5x), to nerozpojíte :)
MareK upraveno: 28. 10. 2020 • 11:45
Zdravím Mozem sa spytat na priklad
tg(x) ^ tg(2x) x ide k PI/4 viem ze to treba prepisat niako na e ^ nieco :D ale dalej neviem :)
dik :)
Dominik Chládek 28. 10. 2020 • 13:31
Dobrý den,
bude to \(e^{\ln \left((\mathrm{tg}x)^{\mathrm{tg}2x}\right)}=e^{\ln \left(\mathrm{tg}2x\cdot \mathrm{tg}x\right)}\) a to budete derivovat jako složenou funkci :)
Klára Těthalová 28. 09. 2020 • 23:56
Zdravím, můžu se zeptat jak na výpočet téhle limity? Nevychází mi ta druhá závorka. Díky moc :)
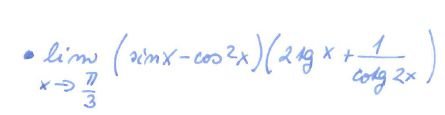
Dominik Chládek 29. 09. 2020 • 08:54
Dobrý den, stačí jenom dosadit pomocí kalkulačky a máte to :)
Dominik Chládek 10. 05. 2017 • 10:16
:D to hodně pobavilo! Budu držet palce, ať to zvládnete :)
kurucr 10. 05. 2017 • 02:22
Ach tie upravy... To chce vela treningu...
