Předpoklady Nesplněny
Derivace součinu funkcíDiferenciální počet (derivace)
-%
Integrální počet (integrace)
-%
Metoda per partes
Řešená cvičení
Integrace s per partes
Vysoká škola • 4 min
Vypočítejte:
\(\displaystyle \int \mathrm{arctg}\;x\; dx\)
Testy
-%
Metoda per partes
Střední škola • 3 min
-%
Příklad -%
Rovnice -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 32 min
Poznámka k videu
V tomto videu si vysvětlíme první integrační metodu a tou je metoda per partes. Pokud integrál nemůžeme vypočítat přímo podle vzorce, pak musíme použít jednu z metod (většinou per partes nebo substituce), díky které získáme jednodušší integrál, případně dokonce integrál který vypočítáme rovnou podle vzorce.
V případě metody per partes se tváříme, že funkce kterou integrujeme se skládá ze součinu dvou funkcí a aplikujeme rozpis, který se opírá o derivaci součinu.
Komentáře
MS 25. 10. 2023 • 10:53
Dobrý den, můžete ukázat, jak se integruje per partes ln^2(x)? Předem díky za odpověď! MS
Dominik Chládek 25. 10. 2023 • 12:42
Dobrý den,
derivovat budete \(\ln ^2x\) a integrovat \(1\) a pak budete postupovat klasicky podle vzorce :) zkusíte začátek?
Dominik
Martin Korda 14. 05. 2021 • 11:15
Dobrý den, na příklad xarctgx jsem použil dvakrát per partes a tímto postupem docházím k jinému výsledku. Prosím, napovíte proč? Viz příloha. Děkuji. Korda
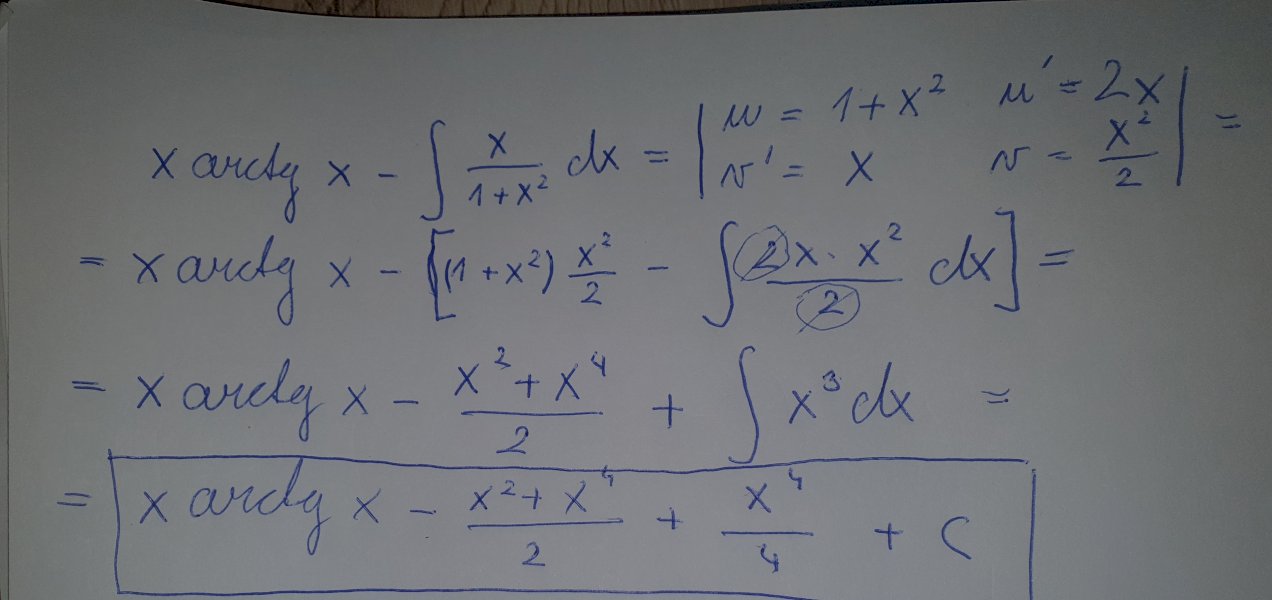
Dominik Chládek 14. 05. 2021 • 22:45
Dobrý den
špatně volíte per partes, \(u=1+x^2\) je špatná volba, takovou funkci tam nemáte, mělo by to být \(u=\dfrac{1}{1+x^2}\) :)
Dominik Chládek 09. 01. 2018 • 10:51
To jsem moc rád, super, držím palce ve studiu! :)
veronika26 07. 01. 2018 • 21:08
Perfektní! Opravdu chválím, vaše videa mě zachránila při učení na zkouškou z Matemtické analýzy 2. Jen tak dál, vše jsem pochopila napoprvé!!!
Dominik Chládek 24. 03. 2017 • 20:49
Díky moc, vážím si pochvaly i odběru :)
WoWce 23. 03. 2017 • 23:32
Díky moc, jste super kanál!! Na YT jsem vám dal subíka. Díky za tvou práci!
Dominik Chládek 01. 08. 2016 • 23:13
Děkuji Vám mnohokrát, jsem moc rád že se videa líbí a že jsou srozumitelná :)
jiricastka 01. 08. 2016 • 12:50
Opravdu, kdyby to přednášejicí na VŠ, nebo učitelé na SŠ vysvětlovali tak jako ty, myslím, že by lidé něměli problém to pochopit ihned napoprvé :).
Dominik Chládek 09. 02. 2016 • 20:06
To je doopravdy velká pochvala, děkuji Vám mnohokrát! Vážím si toho :)
PavlínaBřezinová 09. 02. 2016 • 19:59
Včera nám tuto metodu přednášel profesor matematiky a musím říct, že Vy tu matematiku umíte prostě vysvětlit líp než on - vedoucí ústavu matematiky na fakultě stavební VUT. Děkuji Vám! :)
Dominik Chládek 02. 04. 2019 • 08:48
Dobrý den, to je jenom na Vás co použijete, oba vzorečky fungují stejně, je to jen o tom na co si zvyknete, jednou si zvolte a toho se celou dobu držte :) jinak děkuji!
Veronika Sádovská 01. 04. 2019 • 17:03
Děkuji, konečně mám jasno. Jen ve škole jsme si říkali o trošičku jiný vzoreček: \(\int u^{\prime}vdx=uv-\int uv^{\prime}dx\)
Tímpádem se to celé ztěžuje. Takže nevím podle kterého vzorečku to mám dělat. A to se liší jen jednou přehozenou derivací.
Děkuji předem za odpověď.