Předchozí látkaPředpoklady Nesplněny
Sinus a kosinus jako funkceGoniometrie a trigonometrie
-%
Analytická geometrie
-%
Integrální počet funkcí více proměnných
-%
Transformace do polárních souřadnic
Řešená cvičení
Transformace do polárních souřadnic
Vysoká škola • 6 min
Následující dvojný integrál vypočítejte pomocí transformac do polárních souřadnic:
\(\displaystyle \iint\limits_I\sqrt{x^2+y^2}dxdy\)
\(I:x^2+y^2 \leq 9, y \leq 0\)
Polární souřadnice
Vysoká škola • 7 min
Následující dvojný integrál na oblasti \(I\) vypočítejte pomocí transformace do polárních souřadnic:
\(\displaystyle \iint\limits_I(x^3+xy^2)dxdy\)
\(I:1\leq x^2+y^2 \leq 4, x \geq 0\)
Transformace do polárních souřadnic
Vysoká škola • 14 min
Vypočítejte následující dvojný integrál pomocí transformace do polárních souřadnic:
\(\displaystyle \iint\limits_I xy^2dxdy\)
a) \(I:2y \leq x^2+y^2\leq 4y\)
b) \(I:2y \leq x^2+y^2\leq 4y, x\geq 0\)
Testy
-%
Polární souřadnice
Vysoká škola • 8 min
-%
Substituční rovnice -%
Konkrétní jakobián -%
Podmínka -%
Příklad -%
Podrobnosti o látce
Výpisky ke stažení
Transformace do polárních souřadnic
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
1 h 33 min
Komentáře
PeterFei 03. 01. 2020 • 11:58
Dobry den, ako sa určujú hranice ρ(ró) ak mám e?
je správne: 1≤ρ≤e alebo 1≤ρ≤√e ?
v prílohe posielam príklad
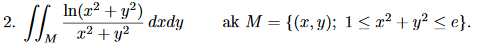
PeterFei 03. 01. 2020 • 17:25
Ďakujem :)
Dominik Chládek 03. 01. 2020 • 15:39
Dobrý den,
má to bý takto:
\(0\leq \varphi \leq 2\pi\\ 1 \leq \rho \leq \sqrt e\)
tedy vaše druhá možnost, jelikož v rovnici kružnice je poloměr na druhou :)
Ing. Ujo Klimek RNDr. 24. 06. 2019 • 19:40
Nemala by mať táto sekcia názov "Transformácia dvojného integrálu"?
Dominik Chládek 28. 11. 2019 • 09:46
Dobrý den, to je chyba, přetočím to, moc děkuji za upozornění! :)
Max Šeffer 27. 11. 2019 • 18:42
V druhém řešeném příkladu chybí Jakobián. Jde o chybu, nebo tam být nemá?
Dominik Chládek 24. 06. 2019 • 22:30
Moc děkuji za doplnění, opraveno :)