Exponenciální rovnice
Řešená cvičení
Exponenciální rovnice
Střední škola • 1 min
Vyřešte v oboru reálných čísel \(\mathbb{R}\) exponenciální rovnici:
\(3^{x-2}=\sqrt{27}\)
Exponenciální rovnice
Střední škola • 6 min
Vyřešte v oboru reálných čísel \(\mathbb{R}\) exponenciální rovnici:
\(16 \cdot \sqrt{(0,25)^{5-\frac x4}}=2^{\sqrt{x+1}}\)
Exponenciální rovnice
Střední škola • 2 min
Vyřešte v oboru reálných čísel \(\mathbb{R}\) exponenciální rovnici:
\(\sqrt[4]{4^x} \cdot \sqrt[3]{2^{x-3}}=\sqrt[6]{16}\)
Testy
-%
Exponenciální rovnice
Střední škola • 4 min
-%
Postup -%
Postup -%
Řešení rovnice -%
Podrobnosti o látce
Výpisky ke stažení
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 47 min
Komentáře
j. 19. 01. 2021 • 21:01
Veľmi Vám ďakujem za pomoc, môžete si na konto pripísať dalšiu 1 ku ;)
Dominik Chládek 20. 01. 2021 • 22:27
To jsem moc rád, děkuji za pochvalu a gratuluji!! :)
Nikita Dotlačil 18. 08. 2020 • 17:48
Dobry den mam dotaz k druhemu prikladu v sekci priklady ktery zacina 16* zkousel jsem si to vypocitat sam a vysel mi jiny vysledek ale odchylil jsem se od vaseho postupu jen v jednom bode a to ve chvili kdy jsem vzal odmocninu z (x+1) na prave strane a prepsal to jako vyraz ^1/2. Vy jste toto ve videu neudelal, chci se zeptat jestli je tento postup nemozny a nebo jsem pocital spatne. Dekuji Dotlacil
Dominik Chládek 19. 08. 2020 • 13:28
Vaše chyba je, že jste použil rovnost:
\((x+1)^\frac12=\dfrac x2+\dfrac 12\)
a to neplatí, umocnění není to stejně jako vynásobení :)
Nikita Dotlačil 19. 08. 2020 • 11:21
Prikladam fotku
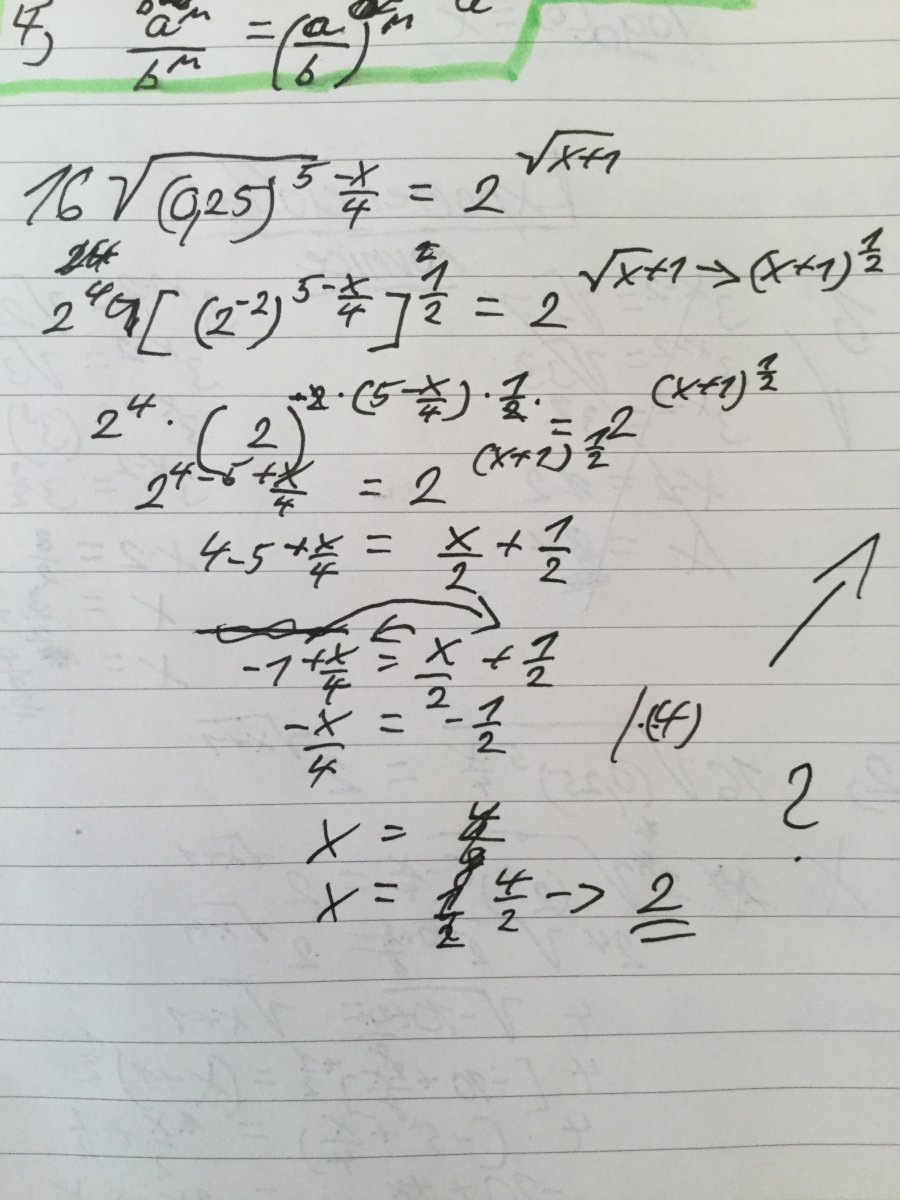
Dominik Chládek 18. 08. 2020 • 22:47
Dobrý den,
pokud chcete volit tuhle cestu, tak jediná šance jak tohle přepsat je:
\(2^{(x+1)^\frac12}\)
a jestli máte tohle, tak to pak už lépe neupravíte, ale musel bych vidět výpočty, tak třeba nahrejte fotku na ukázku a já Vám řeknu jestli a kde je chyba :)
Daniel Drobek 02. 02. 2020 • 15:52
U druhého příkladu (začinající 16*odmocnina z ...) v čase 3:58 nebylo zvoleno špatně známénko u 2ab, kde b je -1 a zapsal si ho jako kladné? Děkuji
Dominik Chládek 02. 02. 2020 • 23:47
Moc děkuji! :)
Daniel Drobek 02. 02. 2020 • 22:52
Už si uvědomuji chybu, omlouvám se. Odvádíš skvělou práci. Díky!
Dominik Chládek 02. 02. 2020 • 18:18
Dobrý den, proč přesně myslíte? :)
Dominik Chládek 28. 09. 2017 • 18:45
Super :)
erorrek 28. 09. 2017 • 13:38
Děkuju, už to asi chápu, to s tím t mi pomohlo)
Dominik Chládek 28. 09. 2017 • 11:41
Dobrý den, zkuste to udělat tak, že si napíšete místo výrazu \(2^x\) třeba \(t\) nebo něco takového :) pak se Vám to třeba lépe uvidí? Protože jinak moc nerozumím...
erorrek 28. 09. 2017 • 03:53
Zdravím, trochu nerozumím vytýkání toho 2^x kolem 20:45, pochopil bych kdyby neznámá nebyla v mocnině pak 2x+2*2x = 2x+4x a když chci vytknout 2x(1+2) = 2x * 3. Ale pokud mám mocninu tak to nemůžu udělat tak že 2^x + 2^x * 2 = 2^x + 4^x takže něak nevím jak na to ..