Předpoklady Nesplněny
Kombinace bez opakováníKombinatorika
-%
Kombinatorika
-%
Vlastnosti kombinačních čísel a rovnice
Řešená cvičení
Jedno kombinační číslo
Střední škola • 3 min
Zapište jedním kombinačním číslem výraz:
\(\begin{pmatrix}15\\14\end{pmatrix}+3\)
Kombinační číslo a rovnice
Střední škola • 6 min
Vyřešte následující rovnici s kombinačními čísly:
\(\begin{pmatrix}x\\x-2\end{pmatrix}-\begin{pmatrix}x+1\\x\end{pmatrix}=4\)
Součet výrazů
Střední škola • 2 min
Zapište jedním kombinačním číslem výraz:
\(1+\begin{pmatrix}21\\20\end{pmatrix}\)
Testy
-%
Vlastnosti kombinačních čísel a rovnice s nimi
Střední škola • 7 min
-%
Definice -%
Podmínky -%
Výraz -%
Výraz -%
Výraz -%
Výraz -%
Podrobnosti o látce
Výpisky ke stažení
Klíčová slova
Kombinatorika Kombinace Kombinační číslo Faktoriál Rovnice VýrazAutor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 44 min
Poznámka k videu
Nyní si zmíníme pár vlastností kombinačních čísel. První vlastnost lehce ověříme rozepsáním podle definice. Platí totiž:
\(\begin{pmatrix}n\\k\end{pmatrix}=\begin{pmatrix}n\\n-k\end{pmatrix}\)
což ověříme lehce rozepsáním definice kombinačního čísla:
\(\begin{pmatrix}n\\k\end{pmatrix}=\dfrac{n!}{k! \cdot (n-k)!}\)
\(\begin{pmatrix}n\\n-k\end{pmatrix}=\dfrac{n!}{(n-k)! \cdot (n-(n-k))!}\) \(=\dfrac{n!}{(n-k)! \cdot (n-n+k)!}\) \(=\dfrac{n!}{(n-k)! \cdot k!}\)
Další vlastnosti jsou co se týče výpočtu. Platí totiž:
\(\begin{pmatrix}n\\0\end{pmatrix}=\begin{pmatrix}n\\n\end{pmatrix}=1\)
\(\begin{pmatrix}n\\1\end{pmatrix}=\begin{pmatrix}n\\n-1\end{pmatrix}=n\)
což znovu můžeme ověřit rozepsání podle definice velmi snadno, proto to sem nebudu rozepisovat :) Tyto výpočty se hodí zejména ve chvílích, kdy počítáme v kombinatorice a nebo pravděpodobnosti nějaké mezi výpočty a nechceme stále rozepisovat dané definice.
Poslední vlastnost kterou si zmíníme je, jak spojit součet kombinačních čísel v jedno kombinační číslo:
\(\begin{pmatrix}n\\k\end{pmatrix}+\begin{pmatrix}n\\k+1\end{pmatrix}=\begin{pmatrix}n+1\\k+1\end{pmatrix}\)
o čemž se můžeme znovu jako i v předchozích případech lehce přesvědčit rozepsáním podle definice kombinačního čísla a poté sečtením takto nově vzniklých výrazů:
\(\begin{pmatrix}n\\k\end{pmatrix}+\begin{pmatrix}n\\k+1\end{pmatrix}\) \(=\dfrac{n!}{k!\cdot (n-k)!}+\dfrac{n!}{(k+1)!\cdot (n-k-1)!}\) \(=\dfrac{n! \cdot (k+1)+n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}\) \(=\dfrac{n! \cdot (k+1+n-k)}{(k+1)!\cdot (n-k)!}\) \(=\dfrac{n! \cdot (n+1)}{(k+1)!\cdot (n-k)!}\) \(=\dfrac{(n+1)!}{(k+1)!\cdot (n-k)!}=\begin{pmatrix}n+1\\k+1\end{pmatrix}\)
Pokud se nám kombinační čísla objeví v rovnici, tak je nejlepší cestou rozepsání těchto kombinačních čísel podle definice a tím převedeme tuto novou situaci na rovnice s faktoriály, o kterých jsme hovořili v minulém videu - tedy na situaci kterou už známe. Ovšem je důležité zmínit, že jeden rozdíl tu je - do podmínek musíme přidat, že v každém kombinačním čísle musí být horní číslo větší nebo rovno tomu dolnímu, tedy máme ještě jednu podmínku k vyřešení navíc.
Komentáře
Jan Kubica upraveno: 22. 04. 2021 • 12:15
Dobrý den, jen drobná nepřesnost ve výkladu. Mám dojem, že kombinační číslo kde k>n můžeme definovat jako n nad k = 0. Protože existuje 0 způsobů, kolik takových skupin po k členech můžeme vytvořit. Ale je to čistě definice a spíše souvisí s kombinacemi, než s kombinačním číslem jako takovým (početně to nejde). Pokud bychom zapomněli na vzoreček a intuitivně bychom vybírali prvky z množiny obsahující n prvků a počítali kombinační číslo jako počet prvků, které mohu vybrat na první pozici v k-členné skupině, k nim pak na druhou pozici, třetí atd. ( pravidlo kombinatorického součinu), tak by nám nakonec došly veškeré prvky v dané množině a na několi pozic v k-členné skupině bychom mohli vybrat přesně nula prvků z dané množiny. Jelikož nula krát cokoliv je nula, tak nás ani nezajímají permutace stejných k-tic, kterými dělíme, abychom získali počet kombinací a říkáme, že n nad k jakožto počet kombinací je roven nule.
Dominik Chládek 23. 04. 2021 • 10:07
Dobrý den, to určitě je možnost, ale řešit v tomto videu na této úrovni (pro středoškoláky) i tyto extrémní případy by bylo z mého pohledu kontraproduktivní, protože by to pak pro někoho mohlo být nepřehledné. To co říkáte bude zmíněno v kurzu na vysokoškolskou kombinatoriku, pravděpodobnost a statistiku :)
Petr Koller 15. 08. 2020 • 13:58
Ještě 1 drobnost, jedná se o malý překlep v testu. Konkrétně u 2. otázky je překlepem slovo jakám
Dominik Chládek 15. 08. 2020 • 19:36
Opraveno, moc díky! :)
Petr Koller 15. 08. 2020 • 13:51
Zdravím, asi po půl hodině bádání nad tím, kde jsem udělal chybu, jsem došel k závěru, že se zadání liší od příkladu ve videu :D
Konkrétně mluvím o posledním video řešeném příkladě, kde v zadání máte na levé straně rovnice mezi dvěma kombinačními čísly znaménko - (mínus), ale ve videu je znaménko +(plus)
Dominik Chládek 15. 08. 2020 • 19:37
Znovu, moc děkuji, opraveno! :)
Jaroslav Máchal upraveno: 06. 05. 2020 • 10:56
Dobrý den, chtěl bych se zeptat na řešení tohoto příkladu. Možná to bude jednoduché, ale nějak jsem se v tom asi zamotal.
Předem děkuji za odpověď
Jaroslav Máchal
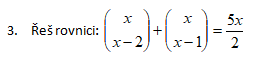
Dominik Chládek 08. 05. 2020 • 22:05
Tak paráda! :)
Jaroslav Máchal upraveno: 08. 05. 2020 • 20:36
Děkuji za odpověď, ale příklad jsem zdárně vyřešil :D
Dominik Chládek 06. 05. 2020 • 23:30
Dobrý den, dejte to do "Příklady od Vás", moc díky :)
Pavel Diviš 23. 04. 2019 • 22:37
Dobrý den, mohl by mi někdo poradit s následujícím příkladem?

Dominik Chládek upraveno: 15. 05. 2019 • 15:07
Dobrý večer, takto:
\(4\begin{pmatrix}n\\2\end{pmatrix}-4\begin{pmatrix}n\\n-3\end{pmatrix}+\begin{pmatrix}n\\3\end{pmatrix}=0\\4\frac{n!}{2!(n-2)!}-4\frac{n!}{(n-3)!3!}+\frac{n!}{3!(n-3)!}=0\\4\frac{n(n-1)(n-2)!}{2!(n-2)!}-4\frac{n(n-1)(n-2)(n-3)!}{(n-3)!3!}+\frac{n(n-1)(n-2)(n-3)!}{3!(n-3)!}=0\\4\frac{n(n-1)}2-4\frac{n(n-1)(n-2)}6+\frac{n(n-1)(n-2)}6=0\\12n(n-1)-4n(n-1)(n-2)+n(n-1)(n-2)=0\\n(n-1)\left[12-4(n-2)+(n-2)\right]=0\\n(n-1)(12-4n+8+n-2)=0\\n(n-1)(18-3n)=0\\n=0,n=1,n=6\)
a z podmínek \(n\geq 3\) máme jen \(n=6\) :)