Předpoklady Nesplněny
Rozklad pomocí vzorcůVýrazy
-%
Funkce
-%
Diferenciální počet (derivace)
-%
Konkrétní výpočet derivace z definice
Řešená cvičení
Derivace z definice
Střední škola • 4 min
U funkce \(f(x)\) spočítejte derivaci v bodě \(x_0\) přímo z definice:
1) \(f(x)=-4x+7,\;x_0=2\)
2) \(f(x)=x^2+3\; x_0=2\)
Derivace z definice
Vysoká škola • 5 min
U funkce \(f(x)\) spočítejte derivaci v bodě \(x_0\) přímo z definice:
\(f(x)=\dfrac2{x+3}, \;x_0\) je libovolné
Derivace z definice
Vysoká škola • 4 min
U funkce \(f(x)\) spočítejte derivaci v bodě \(x_0\) přímo z definice:
\(f(x)=x^3,\;x_0\) je libovolné
Testy
-%
Konkrétní výpočet derivace z definice
Střední škola • 2 min
-%
Definice -%
Definice -%
Výpočet derivace z limit
Vysoká škola • 8 min
-%
Použití definice -%
Alternativní definice -%
Dosazení po definici -%
Poznámka k videu
Cílem tohoto videa je ukázat si, jak se počítají derivace funkcí v nějakém bodě čistě jenom s využitím definice pomocí limity. V pozdější fázi si představíme vzorce, které nám výpočet derivací usnadní a pomocí kterých se vyhneme skutečnému výpočtu limit. Pokud bychom ale vzorce zapomněli, chtěli přesvědčit o jejich správnosti a nebo bychom toužili po tom si je odvodit sami, tak využíváme právě definici derivace a tedy limity.
Komentáře
Alžběta Kadlčíková 31. 10. 2023 • 23:00
Hezký den, v druhém testu u alternativní rovnice je ještě možné vytknout h a to zkrátit na výraz lim (h-2) a dosadit za h=0. Nebo ne? :D Díky
Dominik Chládek 01. 11. 2023 • 12:36
Dobrý den, určitě ano, máte pravdu, jen je to trénink toho přepisu definice, ne přímo výpočet tak proto ta podoba :)
Jeník Perník 16. 05. 2023 • 10:08
Dobrý den, v testu máte použitou alternativni metodu pro vypočet derivace, ale nikde ve videu jsem si nevšiml jeji použití a vysvetleni nechapu kde se tam berou ta cisla bylo by mozne nejake vysvetleni ? Děkuji i podle napovedu v testu jsem porad mimo
Dominik Chládek 16. 05. 2023 • 22:49
Dobrý den, dosadíte místo \(x\) všude \(2+h\) a pak už jenom upravujete :)
Jeník Perník 16. 05. 2023 • 10:12
to rozepsani zavorky s f(x) v citateli chápu, ale nechapu jak se z f(x+h) stane to co tam je :-)
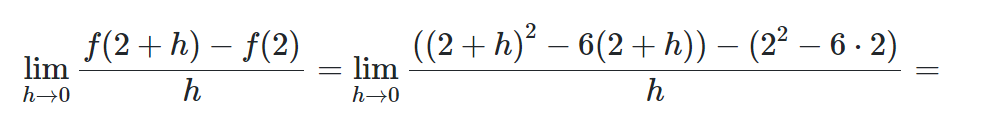
Dominik Chládek 26. 01. 2016 • 12:56
Děkuji Vám mnohokrát za pochvalu :)
sammael 26. 01. 2016 • 11:02
Konečně jsem pochopil, co to vlastně ta derivace je! Děkuji, jste nejlepší. :-)