Předchozí látkaPředpoklady Nesplněny
Průnik množinMnožiny
-%
Množiny
-%
Abstraktní algebra
-%
Monoid, pologrupa a grupa
Návaznosti
Neobvykle definované operaceAbstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Abstraktní algebra
-%
Řešená cvičení
Skládání funkcí
Vysoká škola • 8 min
Rozhodněte, zda se jedná o grupoid, pologrupu, monoid, grupu a nebo komutativní grupu:
\((\{f_1;f_2\}, \circ)\), kde \(f_1(x)=x\), \(f_2(x)=\dfrac1x\) a \(\circ\) je klasické skládání funkcí.
Vlastnosti struktur
Vysoká škola • 10 min
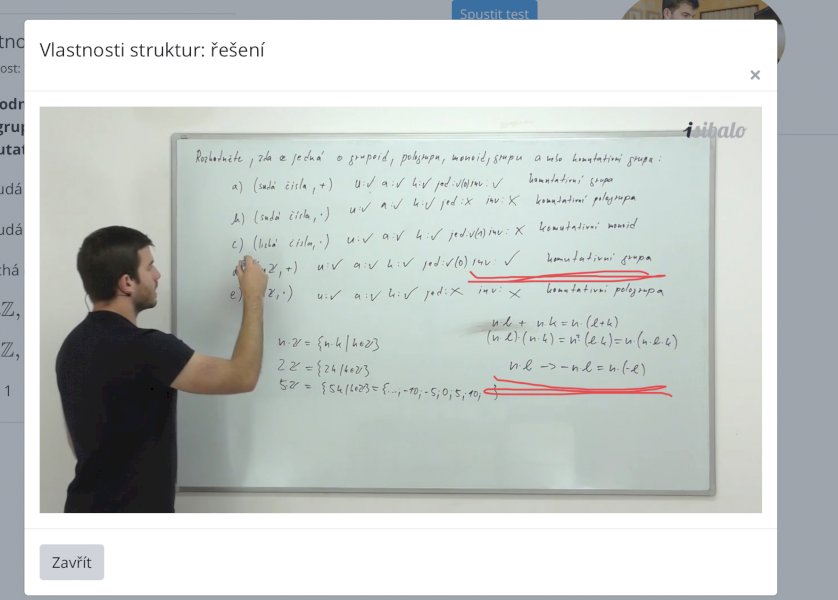
Rozhodněte, zda se jedná o grupoid, pologrupu, monoid, grupu a nebo komutativní grupu:
a) \((\)sudá čísla\(,+)\)
b) \((\)sudá čísla\(,\cdot )\)
c) \((\)lichá čísla\(,\cdot )\)
d) \(( n \mathbb{Z}, +)\)
e) \(( n \mathbb{Z}, \cdot )\)
Testy
-%
Názvy algebraických struktur
Vysoká škola • 4 min
-%
Grupoid -%
Komutativní grupoid -%
Pologrupa -%
Monoid -%
Grupa -%
Abelovská grupa -%
Podrobnosti o látce
Výpisky ke stažení
Monoid, pologrupa a grupa
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 43 min
Komentáře
Kristýna Černotová 28. 08. 2022 • 17:41
Dobrý den,
dá se tedy zjednodušeně říci, že pokud zjistíme, že struktura není asociativní ani komutativní, pak nenalezneme jednotkový ani inverzní prvek?
Mnohokrát děkuji za odpověď.
Dominik Chládek 30. 08. 2022 • 20:12
Dobrý den, pokud nemáte jednotkový prvek tak nejsou ani inverze, ale to že neplatí komutativita nebo asociativita neznamená, že jednotkový prvek nebude :)
Kristina Novotná 09. 01. 2021 • 14:50
Dobrý den, nemělo by být + u daného důkazu ohledně inverzního prvku u příkladu d) ? S pozdravem, Kristína Novotná
Dominik Chládek 02. 10. 2023 • 09:30
Asi máte pravdu :)
Jan 02. 10. 2023 • 08:10
Řekl bych, že to myslela tak, že probíhá důkaz pro (nZ, +), tedy operaci sčítání, ale u důkazu je použito násobení n * l --> -l * n = n * (-l)
Myslím, že operace sčítání nejspíš zmátla, jelikož u (Z, +) se inverzní prvek právě tak dokazoval (2 + (-2) = 0), ale důležité je, že zde nemáme klasickou množinu celých čísel, ale nZ.
Dominik Chládek 09. 01. 2021 • 17:06
Dobrý den,
jak přesně to myslíte? :)