Předchozí látkaPředpoklady Nesplněny
Složitější základní limityLimita a spojitost funkce
-%
Integrální počet (integrace)
-%
Integrály na neuzavřeném intervalu
Řešená cvičení
Integrál s neuzavřeným intervalem
Vysoká škola • 12 min
Vypočítejte:
\(\displaystyle \int_{-\infty}^\infty\frac{dx}{x^2+2x+3}\)
Integrál s neuzavřeným intervalem
Vysoká škola • 5 min
Vypočítejte:
\(\displaystyle \int_{-\infty}^{-4}\frac{dx}{\left(x-2\right)^5}\)
Integrál s neuzavřeným intervalem
Vysoká škola • 8 min
Vypočítejte:
\(\displaystyle \int_0^\infty(3x-4)e^{-3x}dx\)
Testy
-%
Integrály na neuzavřeném intervalu
Střední škola • 8 min
-%
Přepis -%
Přepis -%
Vlastní limita -%
Nevlastní limita -%
Nevlastní limita -%
Limita neexistuje -%
Integrál -%
Neohraničený interval
Vysoká škola • 6 min
-%
Mocnina proměnné -%
Podrobnosti o látce
Výpisky ke stažení
Integrály na neuzavřeném intervalu
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 55 min
Komentáře
Jozo 05. 11. 2025 • 19:21
dobry den, neslo by vyhodnotit tu limitu v cviceniach v 3. priklade ako polinom /exp.(f)=0, mecto toho Lhopitala?
Dominik Chládek 06. 11. 2025 • 10:31
Dobrý den, uřčitě by to šlo, pokud máte tuto úvahu povolenou a bude tomu kdo to upravuje stačit :) problém jenom je, že musíte kdyžtak potom vysvětlit proč to tak je, že je exponenciála rychlejší :)
Matej 28. 09. 2024 • 19:55
dobry den, nemate ve "vypisky ke stazeni" chybu ve vzorcich? nemelo by tam byt napsane spise F(b) - F(a)? ve vypiskach mate napsane F(a)-F(b), ve videu jste pouzil a napsal vzorec na tabuli F(b) - F(a), ale ve vzorcich pod videem to je jinak.
Dominik Chládek 12. 10. 2024 • 18:09
Už jsem je nahrál opravené, moc Vám děkuji ještě jednou :)
Dominik Chládek 10. 10. 2024 • 15:06
Dobrý den, máte pravdu, moc děkuji za upozornění, výpisky jsem zatím stáhnul a nahraji je opravené :)
Nezlobte se za zpoždění s odpovědí, měli jsme chybku na webu a nechodilo nám upozornění na nové komentáře, tak to doháním teď, omlouvám se! :)
Jenda Mařík upraveno: 15. 02. 2024 • 08:13
Dobrý den, co kdybych v posledním příkladu postupoval následovně (viz příloha). je to matematicky korektní? (to = mezi limitou a integrálem na začátku je omyl)
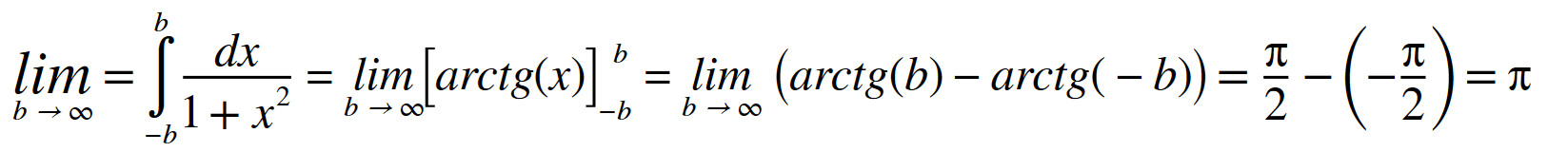
Dominik Chládek 15. 02. 2024 • 15:11
Dobrý den, ano, dalo by se to takto udělat, v tomto speciálním případě :)