Předchozí látkaPředpoklady Nesplněny
Reálná čísla a číselná osaČíselné obory a základní znalosti
-%
Číselné obory a základní znalosti
-%
(Starší) 6. třída - Desetinná čísla
-%
Zobrazení čísel na číselnou osu
V čase 4:03 jsem místo \(\dfrac97\) napsal \(\dfrac 94\), omlouvám se za chybu! :)
Řešená cvičení
Zobrazení odmocniny
Základní škola • 5 min
Zobrazte následující číslo na číselnou osu:
\(-\dfrac{\sqrt3}{4}\)
Zobrazení rozdílu
Základní škola • 3 min
Zobrazte následující číslo na číselnou osu:
a) \(1+\sqrt2\)
b) \(1-\sqrt2\)
c) \(-1-\sqrt2\)
Zobrazení odmocniny
Základní škola • 3 min
Zobrazte následující číslo na číselnou osu:
a) \(\sqrt2-\sqrt3\)
b) \(\sqrt3-\sqrt2\)
c) \(\sqrt2+\sqrt3\)
Testy
-%
Zobrazení čísel
Základní škola • 5 min
-%
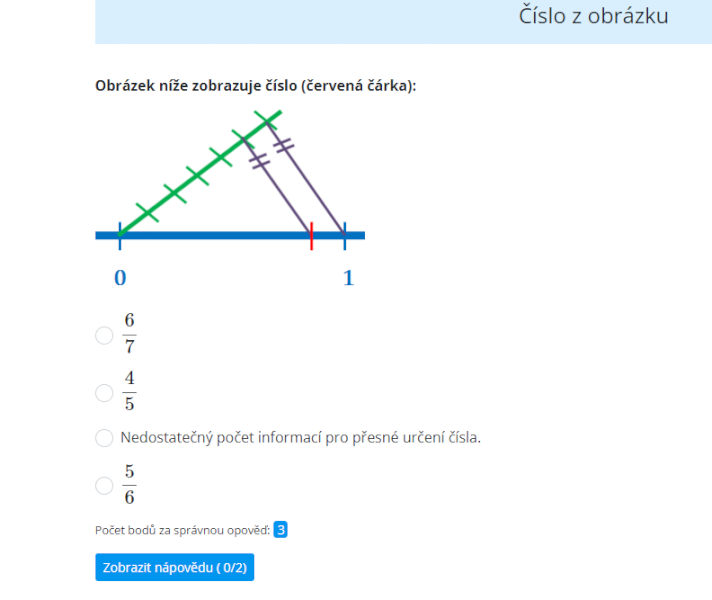
Číslo z obrázku -%
Číslo z obrázku -%
Zobrazení na osu
Základní škola • 6 min
-%
Zlomek -%
Osa -%
Odmocnina -%
Podrobnosti o látce
Klíčová slova
Reálná čísla Racionální čísla Číselná osa Odmocnina Mocnina Zlomek Pythagorova věta Zobrazení Smíšené čísloAutor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Základní škola
Odhadovaná délka studia
0 h 33 min
Poznámka k videu
Číselnou osu využíváme hlavně tak, že na ni zobrazujeme reálná čísla. Nejčastěji se jedná o racionální čísla (zlomky) a odmocniny.
Pokud chceme na číselnou osu zobrazit zlomek, tak si ho nejlépe převedeme na smíšené číslo a od čísla, které reprezentuje počet celků vedeme úsečku, kterou rozdělíme na stejně dlouhé dílky, kterých je tolik, jak velké číslo je ve jmenovateli zlomku. A poté už jenom spojíme příslušný dílek rovnoběžkou, podle zlomkové části.
Pokud chceme na číselnou osu zobrazit odmocninu, tak vedeme kolmici a poté využíváme pythagorovu větu při hledání diagonály o délce dané odmocniny.
Komentáře
Dennis Kovář 22. 10. 2021 • 11:45
Ve videu říkáte, že má být kolmice od osy a k tomu úsečka v libovolném úhlu, která se bude dál dělit na daný počet dílků. V tomto příkladu z testu však není kolmá ta daná úsečka (vpravo). Proč?
Dominik Chládek 24. 10. 2021 • 13:38
Dobře, tak jsem rád že už se chápeme :)
Dennis Kovář 22. 10. 2021 • 11:45
Zrovna mi to došlo :D
Dominik Chládek 05. 12. 2016 • 22:01
Děkuji Vám mnohokrát, jsem rád že se Vám videa líbí a že to začíná zapadat, snad to tak bude i nadále! :)
Grimaudus 05. 12. 2016 • 18:19
Dost dobrý! Po letech matematiky konečně začínají ty dílky zapadat do sebe... Děkuji :)