Určení předpisu zobrazení
Řešená cvičení
Předpis lineárního zobrazení
Vysoká škola • 16 min
Mějte lineární zobrazení \(f:\mathrm{Mat}_{2\times 2}(\mathbb{R}) \rightarrow \mathbb{R}\), kde \(f(A_1)=1\), \(f(A_2)=-2\), \(f(A_3)=3\) a \(f(A_4)=4\). Nalezněte předpis tohoto zobrazení, kde:
\(A_1=\begin{pmatrix}1&-1\\0&0\end{pmatrix}\), \(A_2=\begin{pmatrix}1&1\\0&1\end{pmatrix}\), \(A_3=\begin{pmatrix}1&1\\1&0\end{pmatrix}\), \(A_4=\begin{pmatrix}1&1\\0&0\end{pmatrix}\)
Předpis lineárního zobrazení
Vysoká škola • 12 min
Určete předpis lineárního zobrazení \(\varphi : \mathbb{R}^3 \rightarrow \mathbb{R}^4\) pro které platí:
\(\varphi (1;0;1)=\) \((2;3;1;-2)\)
\(\varphi (0;1;1)=\) \((-2;0;4;1)\)
\(\varphi (0;1;0)=\) \((0;2;0;3)\)
Testy
-%
Předpis lineárního zobrazení
Vysoká škola • 6 min
-%
Předpis zobrazení -%
Předpis zobrazení -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 51 min
Komentáře
David Lefler 18. 08. 2022 • 15:46
Zdravím, dopočítal jsem se k výsledku prvního příkladu stejným způsobem jako Konstantin. přikládám obrázek. Myslíte, že je možné tento přístup používat obecně pro zobrazení z matice do jednoprvkového vektoru?
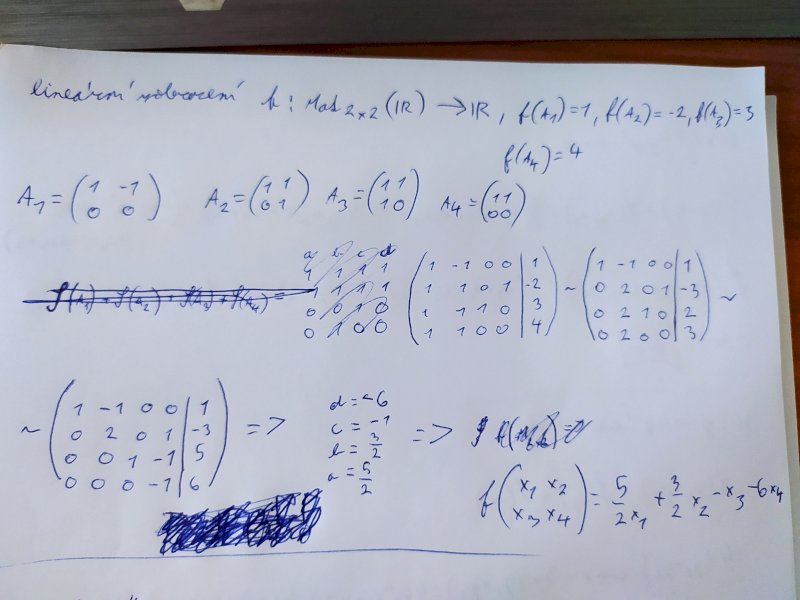
Dominik Chládek 18. 08. 2022 • 20:51
Dobrý den,
jak jsem psal níže, to si úplně neumím představit odkud se bere, očividně Vám to funguje tak to můžete zkoušet, ale jestli jde o (obrovskou) náhodu nebo správný postup, to neumím vysvětlit a proto ani neumím odpovědět, nezlobte se :/
Konstantin 28. 01. 2021 • 09:14
Zdravím, nemůžeme vyřešit př1 z těch řešených tímto způsobem? Dáme matice jako vektory, např. A1=(1, -1, 0, 0) a dáme jich jako řádky do matice. Přes svíslou čáru napišme výsledky zobrazení (k A1 napišíme 1). Tak najdeme koeficienty k tím prvkům. Odpověď je stejná. Ale nevím jestli to půjde v jiných příkladech.
Dominik Chládek 28. 01. 2021 • 12:37
Dobrý den, tak to si úplně neumím představit proč by mělo fungovat...můžete to třeba rozepsat do rovnic, co tím máte přesně na mysli? Protože jestli hledáte linární kombinace, tak ty se tímhle způsobem neřeší....