Předchozí látkaPředpoklady Nesplněny
Složitější per partesIntegrální počet (integrace)
-%
Integrální počet (integrace)
-%
Obě metody dohromady
Řešená cvičení
Obě metody integrace
Vysoká škola • 11 min
Vypočítejte pomocí substituce a potém pomocí per partes:
\(\displaystyle \int \cos^3x\ln\left(\sin x\right)dx\)
Obě metody integrace
Střední škola • 4 min
Vypočítejte pomocí substituce a poté pomocí per partes:
\(\displaystyle \int \dfrac{\ln x}{x}dx\)
Testy
-%
Kombinace metod
Vysoká škola • 3 min
-%
Kombinace -%
Metody dohromady
Vysoká škola • 20 min
-%
Dva logaritmy -%
Exponenciála a odmocnina -%
Logaritmus a odmocnina -%
Podrobnosti o látce
Výpisky ke stažení
Obě metody dohromady
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 41 min
Poznámka k videu
V tomto videu si shrneme obě metody per partes a substituce dohromady. Řekneme si na co se musíme soustředit a co si hlídat.
Komentáře
Daniel 10. 03. 2023 • 23:39
Dobrý den, vysvětlil by mi prosím někdo postup u tohoto příkladu ?
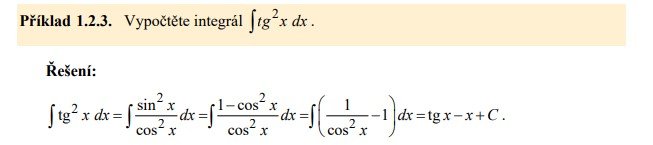
Dominik Chládek 12. 03. 2023 • 10:37
Dobrý den, v čitateli byl využit vzorec pro goniometrické funkce:
\(\sin^2x+\cos^2x=1\\ \sin^2x=1-\cos^2x\)
a pak jenom rozpojeno na dva zlomky a zintegrováno zvlášť přímo podle základních integračních vzorečků :)
MareK 07. 03. 2021 • 18:19
zdravím takáto úloha by sa ako riesila ? :)
integral (Sinx)^4
Dominik Chládek 08. 03. 2021 • 11:06
Dobrý den, mrkněte na trigonometrickou substituci v tomto tématu :)