Integrál s proměnnou pod odmocninou
Řešená cvičení
Proměnná pod odmocninou
Vysoká škola • 4 min
Vypočítejte:
\(\displaystyle \int \dfrac{\sqrt x}{\sqrt x-1}dx\)
Proměnná pod odmocninou
Vysoká škola • 6 min
Vypočítejte:
\(\displaystyle \int \dfrac{\sqrt[3]{x^2}}{\sqrt[3]x+2}dx\)
Proměnná pod odmocninou
Vysoká škola • 6 min
Vypočítejte:
\(\displaystyle \int \dfrac{dx}{\sqrt x+\sqrt[3]x}\)
Testy
-%
Integrál s proměnnou pod odmocninou
Střední škola • 4 min
-%
Substituce -%
Vyjádření -%
Substituce -%
Substituce -%
Substituce za mocninu
Vysoká škola • 5 min
-%
Proměnná pod odmocninou -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 37 min
Komentáře
Ondřej 24. 08. 2023 • 14:02
Moc se omlouvám za spam, chtěl jsem poslat jen jeden komentář...
Ondřej 24. 08. 2023 • 13:59
Dobrý den, mám dotaz k prvnímu příkladu ve videu. V čase 2:08 říkáte, že odmocnina z t na druhou se rovná t, protože mocnina a odmocnina se vyruší, ale já měl za to, že pokud dáme t na druhou a pak je odmocníme, tak dostaneme jeho absolutní hodnotu. Děkuji za objasnění a za skvělá videa!
Petra upraveno: 14. 03. 2023 • 15:11
Zdravím Vás, jen jsem se chtěla zeptat, zda ve druhém příkladě nemáte chybu. Na začátku máte před integrálem 3 a pak se tam objeví 2 a výsledek už je pak jiný... Děkuji za objasnění :-)
heamorhoid upraveno: 01. 06. 2024 • 19:50
Dobrý den. Jaký je prosím výsledek? Je můj správně?
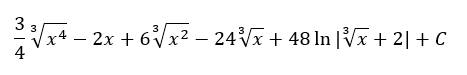
Dominik Chládek 16. 03. 2023 • 14:26
Dobrý den, ano, je to i v poznámce nad videem že je tam chyba, nezlobte se :)