Posuny grafu funkcí sinus a kosinus
Návaznosti
Řešená cvičení
Zatím zde nejsou žádné řešené příklady
Testy
-%
Posuny grafu funkcí
Střední škola • 5 min
-%
Změna periody -%
Vertikální posun -%
Horizontální posun -%
Rozšiřování a zmenšování -%
Podrobnosti o látce
Výpisky ke stažení
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 14 min
Komentáře
Patrik 23. 11. 2021 • 17:26
Dobrý deň,
Mám pocit, že v teste k videu sú zle zadané správne odpovede, dokonca aj v nápovedách.
Napr. "Hodnota d posunuje graf funkce vertikálně (ve směru osy y)." "Hodnota c posunuje graf funkce horizontálně (ve směru osy x)."
Dominik Chládek 28. 11. 2021 • 13:13
Mýlíte se :) zkuste mrknout na PDF k videu :)
Patrik 26. 11. 2021 • 14:33
Dobrý deň
lebo hodnota "c" posúva graf vertikálne (po osi y) a hodnota "d" zväčšuje alebo zmenšuje periódu. Či sa nebodaj mýlim? :)
Dominik Chládek 24. 11. 2021 • 21:57
Dobrý den, proč myslíte? :)
Andrea 25. 01. 2021 • 11:30
Zdravím, zřejmě mám dost podobný dotaz jako Martin, nicméně ani po přečtení komentářů mi to není úplně jasné.
Mám posunout graf do podoby f(x) = sin(x-2), posouvám tedy doprava, ale o kolik, když na ose x mám hodnoty π?
Moc děkuji.
Andrea
Dominik Chládek 25. 01. 2021 • 12:43
Dobrý den,
no tohle úplně přesně nezvládnete, protože ten posun není o násobek pí :) takže víte, že na ose x máte \(\pi=3,14159...\) a podle toho musíte odhadnout, kde bude dvojka, ale dokonale přesně to nikdy nepůjde :)
Martin 30. 12. 2020 • 23:51
Dobrý večer. Mám dotaz jak postupovat, když mám v zadání nakreslit graf a určit Df a Hf funkcí : f(x)= sin (1-x) resp. f(x)= cos (1-x) . ( Jsem trošku zmatený z toho že tam je ( 1-x ) .
Děkuju za odpověd.
Dominik Chládek 31. 12. 2020 • 19:17
Ano, přesně tak :)
Martin upraveno: 31. 12. 2020 • 18:16
Jop. Ja byl zmaten tím že bych tam očekaval nějaký nasobek π. např... sin (x-π) potom by to vychazelo přesně. . čili ten posun pujde doprava ?
Dominik Chládek 31. 12. 2020 • 12:21
Dobrý den,
představte si to jako \(\sin (-(x-1))\) a \(\cos (-(x-1))\), pomohlo? :) je to posun po ose x, takže se ani Df ani Hf nebude měnit :)
xdddddddddddddddddd 13. 08. 2019 • 16:40
Dobrý den, omlouvám se, ale máte mě tu zas. :-D
Chtěl jsem Vás poprosit o pomoc, ale chápu, pokud to není možné.
Do přílohy jsem vložil zadání a výsledek, jen moc nechápu, jak na to přijít.
Moje kroky jsou:
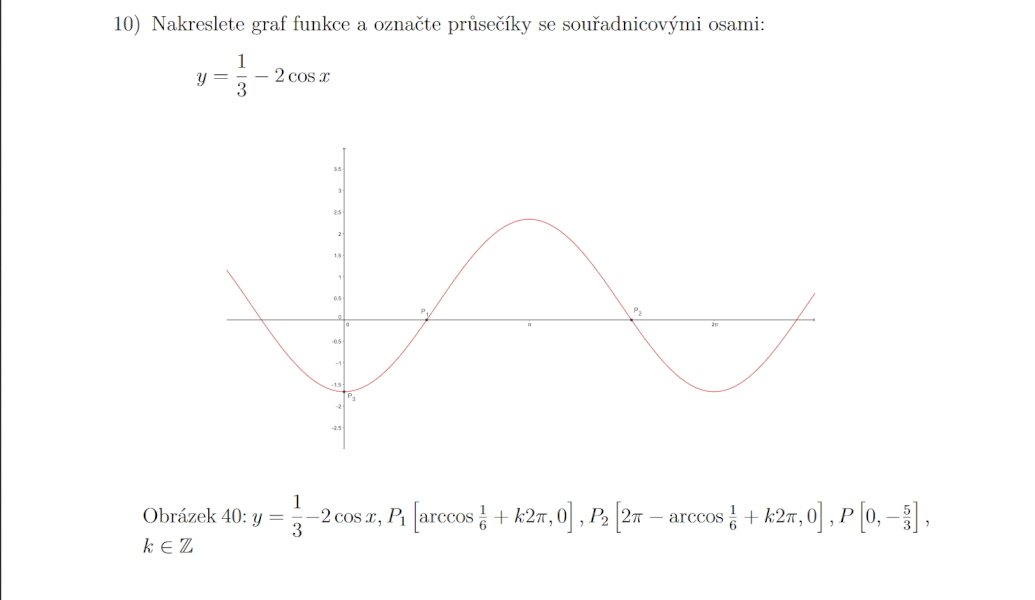
\(y = {1 \ \over 3} - 2cosx\) přepíšu na \(y = - 2cosx + {1 \ \over 3}\)
1. Není tu hodnota "d" a perioda u cos je 2pi
2. Hodnota "a" je záporná, nezměnený cos začíná v max, tenhle začne v min.
3. Zjistím hodnoty max a min.
Max : \({1 \ \over 3} +2 = {7 \ \over 3}\)
Min: \({1 \ \over 3} - 2 = {-5 \ \over 3}\)
4. Hodnota \({1 \ \over 3}\) je hodnota "c" a posune mi osu x o \({1 \ \over 3}\)nahoru
5. Vyřeším rovnici \(y = - 2cosx + {1 \ \over 3}\)
5a) \(- 2cosx = -{1 \ \over 3}\) /vydělím -2
5b) \(cosx = {1 \ \over 6}\) výsledek
Tak a teď, protože \({1 \ \over 6}\)není tabulková hodnota, tak proto mám použít ten arccos?
Dalo by se říct, že to funguje stejně jako v případě "nešikovných" exponenciálních rovnic, kde v některých případech místo hezkého x=2 výjde výsledek jako log=něčeho?
Chápu tedy první Průsečík (trochu), ale co ten druhý? Proč odečítám 2pí ? A chápu dobře, že \({1 \ \over 3}\)je hodnota "c"? V obrázku nic zakresleného nemám. :O
Omlouvám se za delší zprávu, nevěděl jsem, jak to jinak sepsat. Musím říct, že gon. funkce jsem proletěl, nevěděl jsem nic a všechny příklady jsem dal, jen u tohohle posledního si nevím rady, mrknul jsem i na Vaše video o arcos a arcsin, ale nějak to neumím aplikovat. Prosím, poradil byste mi? Případně, měl byste tento měsíc čas i na nějaké doučování přes skype? Děkuji a ještě jednou se omlouvám, za můj sloh. :-)
xdddddddddddddddddd 16. 08. 2019 • 13:08
Jste nejlepší, děkuji! :-)
Dominik Chládek 15. 08. 2019 • 18:37
Ano, máte pravdu, berte tu hodnotu pro arccos jako hodnotu, kde se tak stane a ta hodnota se posouvá o dvě pí tam a zase zpátky, to je ten princip odčítání respektive přičítání té hodnoty. Kdybyste nepřičítal to 2kpí, tak to máte pouze jako jeden jediný bod, nic víc :)
xdddddddddddddddddd 13. 08. 2019 • 23:48
Moc moc děkuji za odpověď! No, na obrázku je dole výsledek, co bych měl napsat do testu.
Měl jsem za to, že P1[arccos 1/6 + k2pi, 0] a p2[2pi - arccos 1/6 + k2pi, 0] a P[0, -5/3] jsou průsečíky. Vždy po nás chtějí, abychom vypsali kdy poprvé funkce protne osu Y a poté, pokud protne osu X, tak vypsat taky a k tomu interval.
Průsečík s osou y mi nedělá problém najít a u funkcí, kterou vyjdou hezky mi nevadí ani průsečíky s osou x, ale v tomhle případě, si nejsem jistý, jak to správně zapsat.
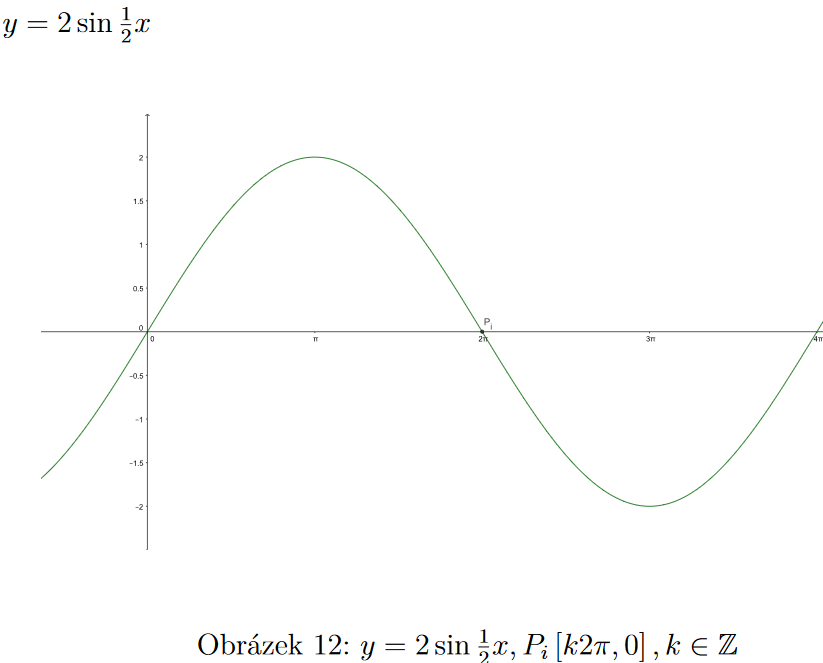
Např. u funkce ( v popisku ) y = 2sin1/2x - před x je 1/2, takže sin vychází z [0,0] nejdřív dosáhne maxima, půjde dolů a osu x protne až v 2pi(místo už v Pi, kdyby nic před x nebylo), další průsečík by byl ve 4pi, pak v 6pi atd. - to máme zapsat do testu.
U té funkce s arccos je to zapsané ale nějak jinak, chápu zapsání P1, ale u P2 jsem nepochopil, proč najednou odečítám a proč to tam vůbec je.
Resp. tuším, že funkce arccos je omezena a nemá Df = R, jako cos, proto je tam to 2pi - arccos 1/6 + k2pi? Protože by to uteklo z df toho arccos? Nebo jsem úplně mimo?
Omlouvám se, ale nevím, jak jinak se vyjádřit. :-(
Dominik Chládek 13. 08. 2019 • 23:18
Dobrý večer,
vůbec se neomlouvejte, moc rád pomohu! Co píšete je přesně správně a hodnotu \(\dfrac16\) doopravdy z hlavy neurčíte, bud ji zapíšete jako \(\mathrm{arccos}\left(\dfrac16\right)\) a nebo si pomůžete kalkulačkou a prostě ji vypočítáte a zaokrouhlíte, jiná šance není :)
Jinak tomu s průsečíkem moc nerozumím, jak přesně to myslíte? Tahle funkce se neposouvá vlevo ani vpravo, takže je sudá, tedy průsečíky s osou x budou symetrické podle počátku a průsečík s osou y bude v tom minimu, které jste perfektně našel :)
Dominik