Předchozí látkaPředpoklady Nesplněny
Vázané extrémy speciální typDiferenciální počet funkcí více proměnných
-%
Vázané extrémy a Lagrangeova funkce
Řešená cvičení
Lagrangeova funkce
Vysoká škola • 7 min
Nalezněte lokální extrémy následující funkce dvou proměnných:
\(f(x;y)=5-x-y\)
s vazebnou podmínkou \(x^2+3y^2=12\)
Metoda Lagrangeových multiplikátorů
Vysoká škola • 21 min
Nalezněte lokální extrémy následující funkce dvou proměnných:
\(f(x;y)=3xy-y^2\)
s vazebnou podmínkou \(x^2+2xy+2y^2=10\)
Lagrangeova funkce
Vysoká škola • 8 min
Nalezněte lokální extrémy následující funkce dvou proměnných:
\(f(x;y)=x^2+2y+y^2\)
s vazebnou podmínkou \(x^2+y^2=9\)
Testy
-%
Vázané extrémy a Lagrangeova funkce
Střední škola • 1 min
-%
Funkce -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
1 h 17 min
Komentáře
Filip 17. 01. 2022 • 22:23
Dobrý den. Prvně bych chtěl poděkovat za super videa. A ted´ bych měl dva dotazy.
1) Dala by se tato funkce počítat pomocí Jacobiho Determinantu ? Máte Video na Jacobiho Determinant ?
2) Jak zjístím z Lagrangovy funkce body kde nabívá minima a maxima?
Děkuju
Dominik Chládek 20. 01. 2022 • 16:16
Dobrý den, moc díky! :)
1) Nemám bohužel na tohle téma video :/
2) Stejným způsobem jako klasicky, jak je to ve videu :)
Adam Babulík upraveno: 02. 01. 2022 • 16:44
Dobrý den,
chtěl bych se zeptat zda-li dojdeme ke stejným výsledkům užitím Lagrangeova multiplikátoru.
Ve škole nás učí tímto způsobem, ale ten váš mi přijde jednodušší.
Děkuji za odpoěď.
Daniel 03. 06. 2021 • 12:01
Dobrý den, chtěl bych se zeptat k řešenému příkladu. Při řešní bodu B s lambdou 1/6e^3 mi vychází v prvním členu Hessovy matice e^-3 + 1/3e^3. Chyba může být na mé straně, ale chtěl jsem se jenom ujistit
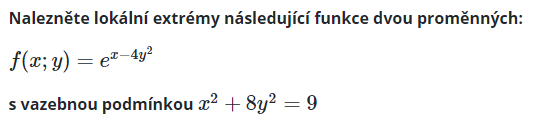
Daniel 05. 06. 2021 • 08:29
Vůbec nic se neděje. Děkuji moc za ujištění :)
Dominik Chládek upraveno: 04. 06. 2021 • 11:37
Dobrý den,
máte pravdu, má tam být plus, špatně jsem dosadil, nezlobte se :) tím pádem vyjde záporná hodnota determinantu a bude se jednat o sedlový bod, už jsem to k příkladu přidal jako opravu :)
Děkuji za upozornění!
Lukas Dufek 29. 05. 2020 • 13:43
Dobrý den, chtěl bych se zeptat jestli se nějak liší postup (popřípadě jak), pokud je ve vázané podmínce absolutní hodnota? Například zde:
Děkuji
Dominik Chládek 29. 05. 2020 • 23:21
Dobrý den, liší, to si musíte zakreslit a vyjadřovat ty hranice postupně, nejde použít přímo Lagrangeovu funkci :/ musíte jít hranici po hranici :)
Karel Suchomel 09. 05. 2020 • 20:38
Dobrý den, měl bych dotaz k jedné úloze, kterou jsou dostal za úkol. Použil jsem na to Langrageovu větu a vyjádřil si 3 parciální derivace pro x, y a lambdu, ale nedokážu se dostat přes soustavu rovnic těchto derivací. Ocenil bych jakoukoliv zpětnou vazbu.
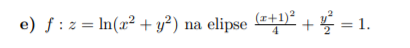
Dominik Chládek 11. 05. 2020 • 23:26
Dobrý den,
dejte to do sekce "Příklady od Vás" a nahrajte k tomu Váš postup do komentářů a podíváme se na to :)
mobiletomik 22. 08. 2019 • 13:23
Dobrý den, nemáte nějaké příklady s výsledky na vázané extrémy a globální extrémy.
Například tohoto typu.
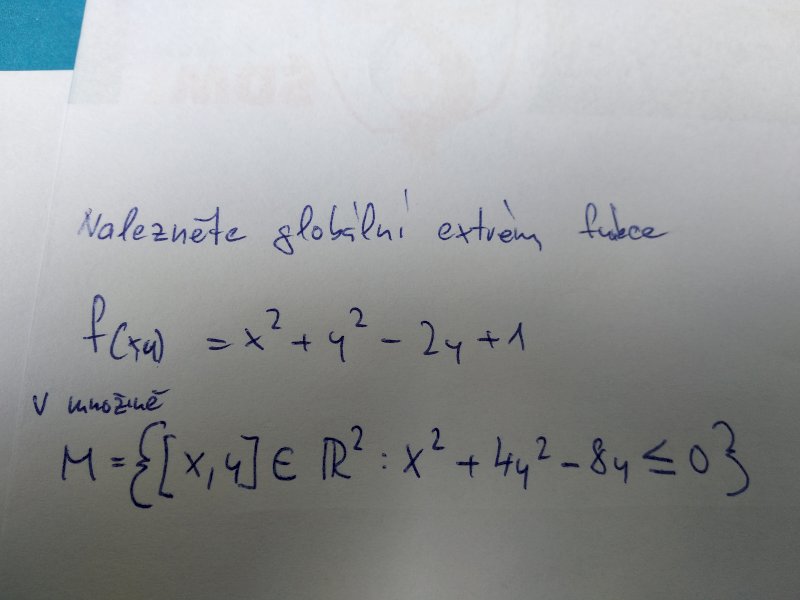
Dominik Chládek 22. 08. 2019 • 13:46
Dobrý den, na webu zatím ne, nezlobte se :/ ale přidám na toto téma videa brzy! :)
Jiří Boleček 26. 04. 2019 • 20:34
Dobrý den, dá se tímto způsobem řešit pře Lagrangeovu funkci i příklad s dvěma podmínkama ?
Dominik Chládek 26. 04. 2019 • 23:18
Dobrý den, a jaké dvě podmínky máte? Nedají se zakomponovat v jednu?