Předchozí látkaPředpoklady Nesplněny
Výpočet jednostranných limitLimita a spojitost funkce
-%
Diferenciální počet (derivace)
-%
Mají všechny funkce derivaci v každém bodě?
Návaznosti
Řešená cvičení
Zatím zde nejsou žádné řešené příklady
Testy
-%
Mají všechny funkce derivaci v každém bodě?
Střední škola • 2 min
-%
Definiční obor -%
Definiční obor -%
Derivace teoreticky
Vysoká škola • 3 min
-%
Spojitost funkce -%
Derivace -%
Podrobnosti o látce
Výpisky ke stažení
Mají všechny funkce derivaci v každém bodě?
Klíčová slova
Derivace Spojitost Funkce Limita Zleva Zprava Absolutní hodnota Vlastní NevlastníAutor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Vysoká škola
Odhadovaná délka studia
0 h 24 min
Poznámka k videu
V tomto videu si odpovíme na otázku, jestli má každá funkce derivaci v každém bodě. Odpovědí je, že ne každá funkce má derivaci v každém bodě. V tomto videu si ukážeme, že ani pojem spojitosti ("nepřerušení funkce skokem") nestačí k tomu, aby funkce derivaci měla. Například, jak si ukážeme, funkce \(f(x)=|x|\) nemá derivaci v bodě \(x_0=0\) i přesto, že je korektně definovaná pro libovolné reálné číslo. Podobně funkce \(f(x)=\sqrt[3]{x}\) má v bodě \(x_0=0\) derivaci rovnu nekonečnu (tedy nevlastní) i přesto, že je definovaná pro libovolná reálná čísla. Derivace pro nás tedy není úplně samozřejmost a pro "hezké" funkce ze se střední školy.
Komentáře
Jozef 29. 08. 2020 • 18:11
Splnuje funkcia |x| definiciu o spojitosti funkcie, ktora bola uvedena vo videu ? Lebo mam pocit, ze nie, kedze nam limita v bode 0 vyjde, ze neexistuje a tym padom sa nerovna funkcnej hodnote v tomto bode, coz je 0 a z toho mi plynie, ze funkcia |x| nie je spojita. Mohli by ste mi povedat, kde je v tejto uvahe chyba?
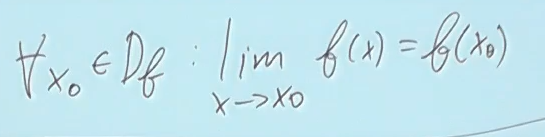
Jozef 30. 08. 2020 • 11:23
Aha. Dakujem za vysvetlenie.
Dominik Chládek 29. 08. 2020 • 22:50
Dobrý den,
proč myslíte, že limita v bodě nula neexistuje? :) když ji zkusíme vypočítat, tak máme:
\(\displaystyle \lim_{x \to 0} |x|=|0|=0\)
a to je to stejné, jako funkční hodnota, tedy tato funkce je spojitá v nule. Asi si to pletete s tím, že tato funkce nemá derivaci v bodě nula :)
dominikklon 13. 01. 2020 • 19:48
V testech je, že derivace funkce 3. odmocnina z x v bode 0 neexistuje. Ale nekonečno je snad existující hodnota ne? :d
Dominik Chládek 16. 01. 2020 • 12:47
Dobrý den, opraveno na "vlastní", moc děkuji za poupravení :)
Dominik Chládek 03. 05. 2016 • 17:49
Jsem rád že pobavilo :D
DoctorSLiME 02. 05. 2016 • 18:56
"Derivace pro nás není samozrejmost" :D Skoro som sa rozplakal :D :D :D :D :D :D
