Převod mezi zadáními
Návaznosti
Řešená cvičení
Rekurence
Střední škola • 2 min
Určete rekurentně posloupnost:
\(\left(\dfrac{1}{n(n+1)}\right) _{n=1}^\infty\)
Testy
-%
Konkrétní převody
Střední škola • 12 min
-%
N-tý člen -%
N-tý člen -%
Rekurence -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 40 min
Poznámka k videu
V tomto videu si ukážeme jak převádět mezi vzorcem pro n-tý člen a rekurentním zadáním a naopak. Ve skutečnosti je to náročný proces a ne každou posloupnost jde snadno převést. Ovšem my si to ukážeme na pár typickým příkladech, abychom měli základní návod, kterým se řídit u ostatních příkladů.
Komentáře
Klaus.Mikaelson 10. 04. 2020 • 12:16
Mohu poprosit o doplnění nebo spíš opravu. Nevím si rady se znaménkama.
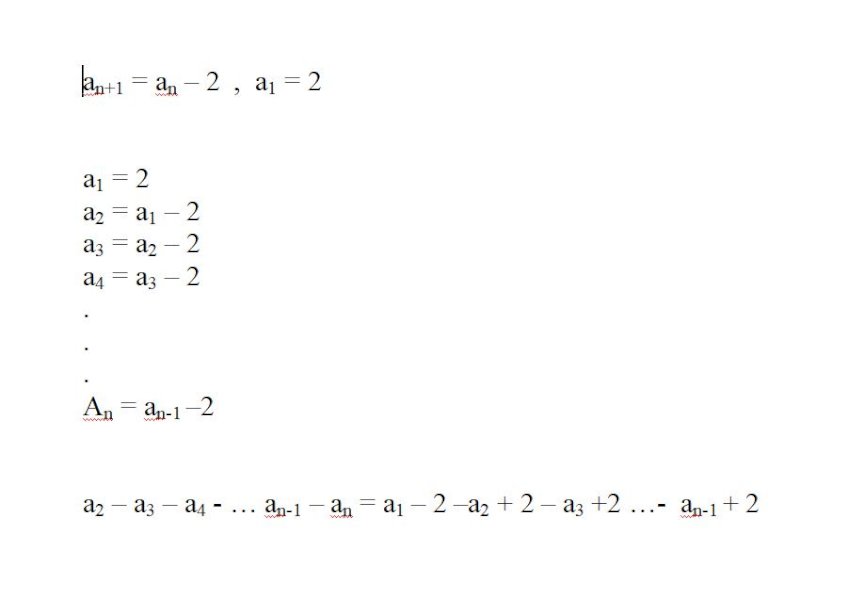
Dominik Chládek upraveno: 10. 04. 2020 • 13:12
Dobrý den,
tak platí:
\(a_2+a_3+a_4\;+\;...\;+\;a_n\)
\(=a_1-2+a_2-2+a_3-2+\;...\;+\;a_{n-1}-2\)
tedy:
\(a_n=a_1+(n-1)\cdot (-2)\)
tedy:
\(a_n=2-2n+2\\ a_n=4-2n\)
a to je výsledek :)
Klaus.Mikaelson 09. 04. 2020 • 13:49
Zdravím, a co když se mi tam vyskytuje součin i součet?
Klaus.Mikaelson 09. 04. 2020 • 18:09
Já žádný konkrétní příklad nemám. Ptal se na to i jeden uživatel v komentářích na youtube, ale odkaz jsem nikde nenašel. Ptal se konkrétně na An+1=2an+3 , a1= -1
Dominik Chládek 09. 04. 2020 • 15:01
Dobrý den, jak přesně to myslíte, máte nějaký konkrétní příklad? :)
Jozef upraveno: 15. 07. 2019 • 16:58
Mám otázku k príkladu, ktorý je uvedený k tomuto videu v sekcii rešené príklady. V tomto príklade sme mali vyjadrit postupnost rekurentne. Vo finálnom riešení (rekurentnom vyjadrení) sa však nachádza premenná n a nerozumie, čomu sa táto premenná v tomto prípade rovná.
Jozef upraveno: 16. 07. 2019 • 14:13
Ďakujem za odpoveď.
Dominik Chládek 15. 07. 2019 • 18:07
Dobrý den, ta se vždy rovná tomu, co za člen chcete zjistit. Takže pokud například hledáte \(a_2\), tak n je jednička, pokud \(a_9\), tak n je pro změnu osm :)
milos 02. 07. 2019 • 13:13
Ďakujem velmi pekne
milos 01. 07. 2019 • 11:25
Zdravím. Chcel by som sa opýtať, akým spôsobom postupovať v prípade, kde sa násobi aj sčíta pri prevode postupnosti z rekurentného do N-tého zadania. Ďakujem za prípadné objasnenie.
Dominik Chládek 02. 07. 2019 • 10:48
Při rozepsání členů máme toto:
\(a_1=1\\ a_n=1+2a_{n-1}\\ -----\\ a_2=3\\ a_3=7\\ a_4=15\\ a_5=31\\ a_6=63\)
což lehce vidět dává:
\(a_n=2^{n}-1\)
a můžeme se přesvědčit že to jde:
\(a_n=1+2a_{n-1}\\ 2^n-1=1+2\cdot (2^{n-1}-1)\\ 2^n-1=1+2^{n}-2\\ 2^n-1=2^{n}-1\\ 0=0\)
milos 01. 07. 2019 • 16:36
a1=1, an=1 + 2an-1
Dominik Chládek 01. 07. 2019 • 15:45
Dobrý den, a máte konkrétní příklad? Protože dost záleží na tom, jak ten příklad vypadá :)