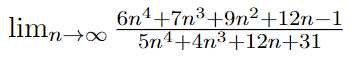Příklady od Vás: Důkaz limity z definice

A.G. 07. 12. 2021 • 18:40

Pýtal som na inom matematickom fóre. Nebolo to priamo na tento príklad. Spoločne sme dospeli k tomu záveru, čím by som túto tému uzatvoril:

- V jednoduhších prípadoch môžeme urobiť dôkaz priamo  z definíce. Našim cieľom nie je nájsť konkrétny index n0, ale ukázať, že taký index existuje. To dokážeme priamo z definície. Potom samozrejme môžeme použiť úpravy, aby sme pri nami ľubovoľne zvolenom epsilóne väčším než nula našli ten index.
- Aby sme nemuseli zakaždým dokazovať existenciu limity postupnosti, využijeme už spomínané vety o konvergentných postupnostiach. To je vhodné napríklad v tomto prípade. Opäť, nebudeme hľadať konkrétny index, ale ukážeme, že ten index existuje. To je zmysel viet. Doslova nám uľahčia život :) Existenciu indexu ukážeme takto: použijeme vety o konvergentných postupnostiach. Takto zložito napísanú limitu "rozdelíme" na menšie limity. A tieto menšie limity už vieme dokázať. To znamená, že sme ukázali existenciu indexu.

tyldonald 06. 12. 2021 • 21:08

Chápu, celé to je zkrátka taková delší piplačka.

A.G. upraveno: 06. 12. 2021 • 07:35

Nechal som si všetky súvislosti uležať v hlave, nakreslil niekoľko grafov v Geogebre. Dospel som k tomuto záveru:

- pomocou viet o limitách postupnosti vieme tento príklad vypočítať rôznymi spôsobmi

- po aplikovaní viet "rozdelíme" celú limitu na niekoľko limít. Každú limitu vieme dokázať priamo z definície, ALE...

- keď chceme dokázať pomocou definície, že limita je 6/5, musíme použiť pôvodné zadanie.

tyldonald upraveno: 05. 12. 2021 • 12:15

Děkuji,

mohl bych se tedy zeptat, jestli tento postup, který jsem použil posledně, akorát teď jsem ho trochu upravil je úplně špatně?

Pouze mě zajímá, zda by to takto nešlo.

A.G. upraveno: 04. 12. 2021 • 18:19

Stále sa snažím nájsť čo najviac jednoduchý spôsob, ako to vyriešiť. Napadlo ma urobiť toto:

1. V čitateľi i v menovateľi vyjmem pred zátvroku najvyššiu mocninu n-ka.
2. Čitateľ i menovateľ je v tváre súčinu - môžeme krátiť.
3. Použijeme vetu o podiely dvoch limít. Takto získame limitu postupnosti  v čitateľi i limitu postupnosti v menovateľi.
4. Na čitateľ i menovateľ aplikujeme vetu o súčte limít. Tým to celé zjednodušíme a vypočítame, že čitateľ má hodnotu 6, menovateľ má hodnotu 5. To znamená, že sme dostali 6/5. 

A teraz, ako to dokážeme? Budeme postupne dokazovať jednotlivé limity postupnosti. To je skôr cvičenie, pretože my už poznáme niektoré vety o konvergentných postupnostiach. 

Skúste ďalej Vy sám :)

A.G. upraveno: 03. 12. 2021 • 20:47

Výraz v absolútnej hodnote je záporný. To znamená, že výsledkom absolútnej hodnoty bude...? :) 

Alebo aj takto:

V čitateli máme záporné číslo. Menovateľ bude vždy kladný, v tomto prípade. Celý zlomok je teda záporný. Vyňajme -1 pred zlomok. Potom využijeme vlastnosť absolútnej hodnoty pre súčin. Mínus 1 bude v absolútnej hodnote, čo znamená, že výsledkom bude 1. Zlomok bude celý kladný. Takto odstránime druhú absolútnu hodnotu.

Teraz skúste ďalej Vy :)

tyldonald 03. 12. 2021 • 18:52

Myslíte si, že takhle by to mohlo být správně? Nebo jsem spočítal totální blbost? Trochu mě trápí ten zeleně označený výsledek dole , čemu se rovná n v závislosti na epsilo, protože mi přijde hodně zvláštní, že je záporný. Ono dost pravděpodobně jsem asi neměl odstraňovat tu absolutní hodnotu. Ale nejsem si raději jistý. :)

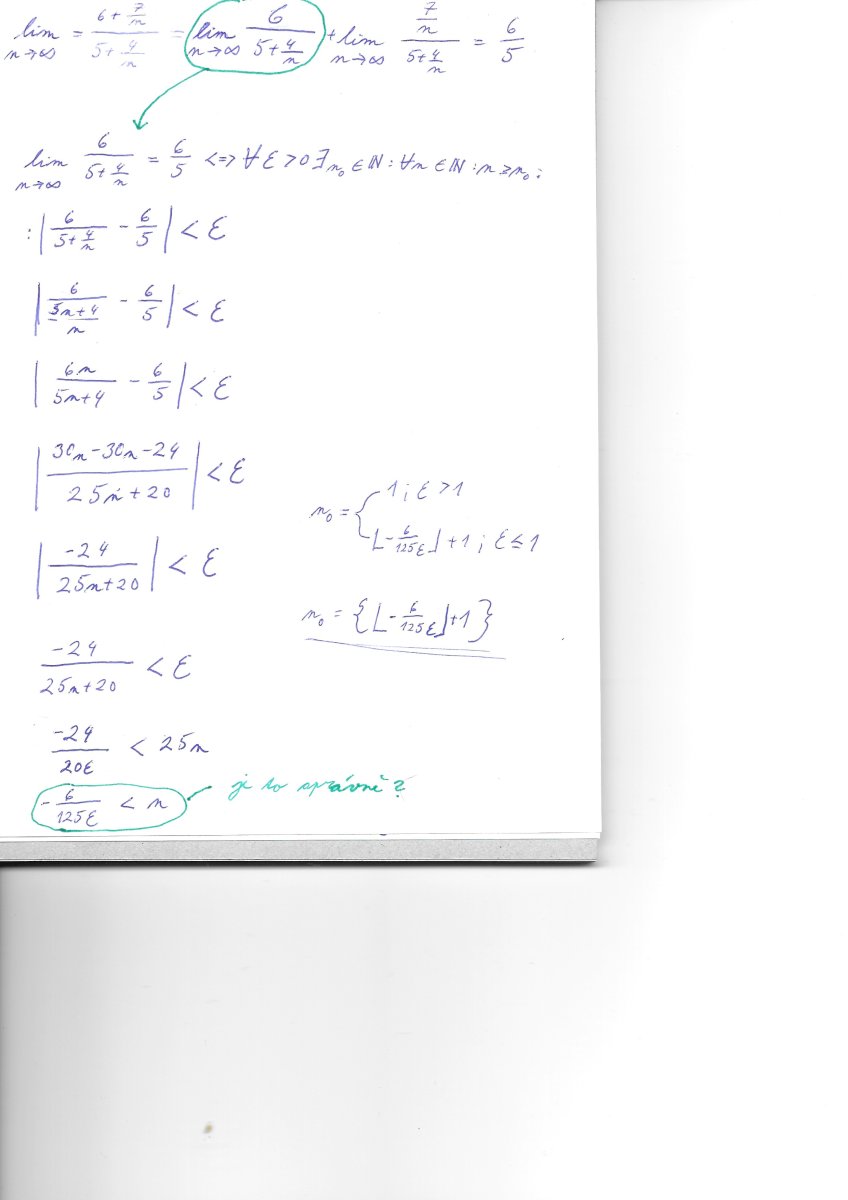
A.G. 03. 12. 2021 • 06:24

Už som na to prišiel 🙂 Neviem, prečo som si to neuvedomil skôr.

1. Zlomok v našom prípade vynásobíme najvyššou mocninou n-ka. Dôvod: máme divergentné postupnosti, potrebujeme ich upraviť na konvergentné.

2. Využijeme vety o limitách konvergentných postupností. Dostaneme súčet niekoľkých limít, viď predošlé príspevky.

3. Prvá limita má hodnotu 6/5, všetky ostatné majú hodnotu 0. To, že konvergujú k nule vieme podľa vety o postupnostiach - netreba ďalej dokazovať.

4. Súčet 6/5+0+0+...+0 = 6/5. Dokazujeme LEN prvú limitu v súčte. To v praxi znamená, že sa nám celý dôkaz značne zjednodušil.

🙂

A.G. 02. 12. 2021 • 08:54

Pýtal som sa na inom matematickom fóre. Tiež to nevidia príliš jednoducho :)

Každopádne, dôkaz chcem urobiť aj ja. Považujem to za cvičenie.

Napadlo mi pohrať sa s tým, skúšať. Začal by som odtiaľto: \(\lim_{n \to \infty } = \frac{6n^{4}+7n^{3}}{5n^{4}+4n^{3}}\)

Vyňať najvyššiu mocninu n-ka pred zátvorku, potom skúšať ďalej. Logicky je vidieť, že zlomok je kladný. Tým pádom môžeme odstrániť absolútnu hodnotu a počítať nerovnicu ďalej. Limita bude stále 6/5. Akurát, že sa bude meniť index, od ktorého budú všetky členy až donekonečna ležať v epsilonóvom páse od originálneho zadania. Postupne by som skúšal ďalej....

A.G. 01. 12. 2021 • 21:06

Skúsil som WolframAlpha, viď odkaz: https://www.wolframalpha.com/input/?i=%286n%5E4%E2%88%927n%5E3%2B9n%5E2%2B12n-1%29%2F%285n%5E4%2B4n%5E3%2B12n%2B31%29

Momentálne ma nenapadá žiaden rozumný spôsob, ako to vypočítať... Možno, že nám Dominik pomôže :)

tyldonald 01. 12. 2021 • 20:20

Chvíli jsem teď nad tím přemýšlel, ale pokud se nemýlím, tak zde dělit polynomy nemohu, jelikož nemohu dělit  polynom nižšího řádu polynomem vyššího řádu. Ale možná si to jen špatně pamatuju.

Takže bych ještě mohl zkusit vytíkat n, ale bojím se, že by to moc nepomohlo.

A.G. 01. 12. 2021 • 14:52

Zatiaľ som to nepočítal, avšak určite si to ako cvičenie spravím.

Skúste celý zlomok upraviť. Napríklad podiel polynómov.

tyldonald 01. 12. 2021 • 13:59

Děkuji,

otázka teď je, jak pokračovat dál. Pokud dobře hádám, tak si nějak musím vyjádřit, čemu se rovná n. Z tohohle bohužel nevím, jak ho vyjádřit pokud jsem někde neudělal chybu.

A.G. upraveno: 01. 12. 2021 • 06:39

Poznáme limitu postupnosti a limitu funkcie. V zadaní ste uviedli limitu postupnosti, čo poznáme podľa premennej n. 

Postupnosť môže konvergovať, t.j. má limitu. Limita je konkrétne reálne číslo, v našom prípade je to 6/5.

Postupnosť, ktorá nemá limitu, sa nazýva divergentná.

Vy spomínate vlastnú limitu v nevlastnou bode. To by sme sa bavili o limite funkcie :)

Pozrime sa ešte raz na príklad zo zadania: chceme vypočítať limitu tejto postupnosti. Ako ste už ukázali na papieri, výpočet nie je taký jednoduchý. Práve preto máme k dispozícii vety o limitách postupnosti, vďaka ktorým limitu ľahko vypočítame :) 

Pokiaľ chcete pomocou definíci dokázať, že uvedená postupnosť má limitu 6/5, musíte počítať ďalej. Správna cesta je označená na Vašom papieri zelenou farbou pera :)

tyldonald upraveno: 30. 11. 2021 • 23:09

Teď si všímám, že jsem použil název špatné definice. Ale jinak pokud se nemýlím, tak toto je vlastní limita v nevlastním bodě, kterou jsem měl použít?

Jinak jako tu funkci volím tu, kterou jsme si upravili v krocích před tím pokud se nemýlím, protože při dosazení do původní bych dostal otřesné číslo, jelikož tam je polynom čtvrtého stupně a tak dále.

Pokud jsem tedy počítal dobře ( ale je pravděpodobné, že jsem se mohl upočítat), tak teď si úplně nejsem jistý, jak vyjádřím z nerovnice to n, jelikož mi to nějak nevychází.

Ale kdybych to upravoval dál tak by mi vyšlo, že 121/360epsilon je menší jak jedna a to by možná už nějaký smysl dávalo. Ale jistý si nejsem a možná vymýšlím trochu blbosti.

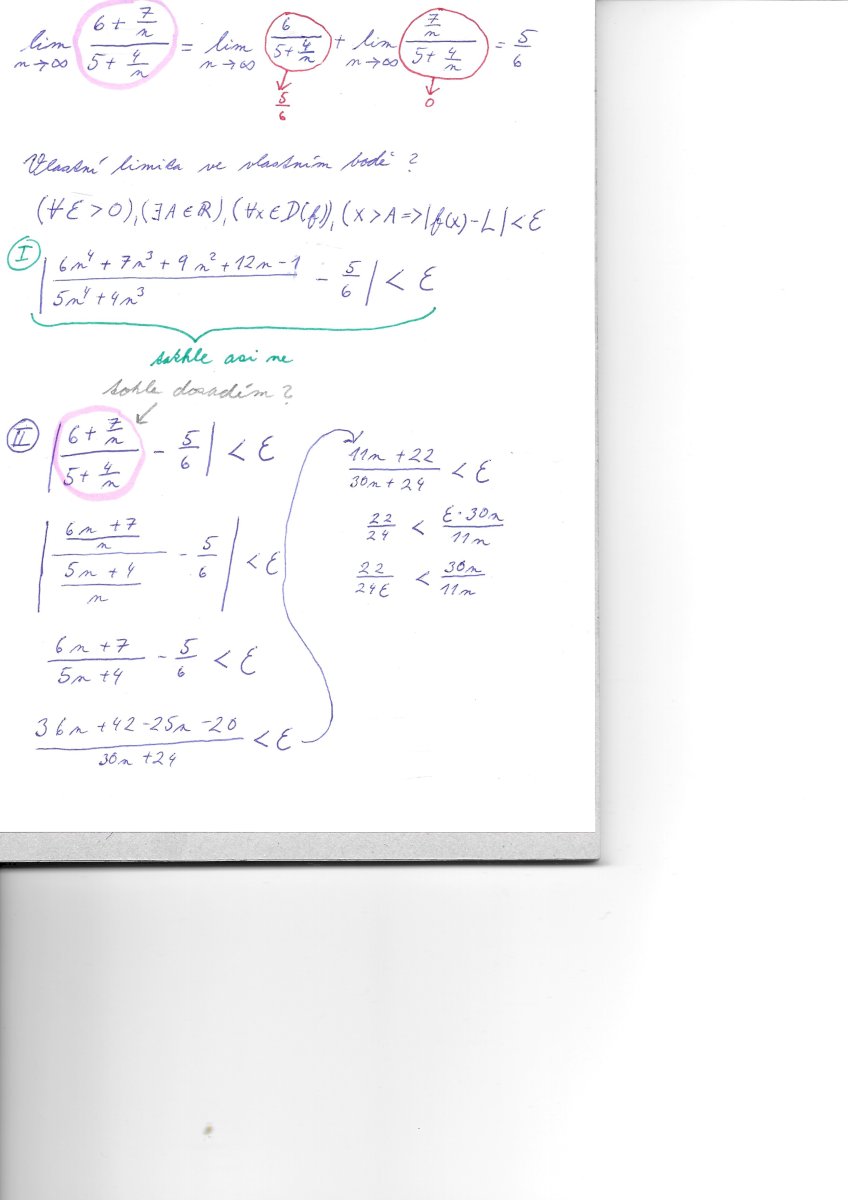
A.G. upraveno: 30. 11. 2021 • 21:51

Výborne! Máte výsledok :) Teraz k dôkazu: do definície dosadíme za L = 6/5. Odstránime absolútnu hodnotu. Nerovnicu upravíme. 

tyldonald 30. 11. 2021 • 21:40

Pokud jsem tu větu dobře pochopil, tak bych to napsal takto. Z té první limity vidím, že se se bude rovnat 6/5 a druhá se bude rovnat 0. Takže po součtu bude výsledek 6/5.

A.G. upraveno: 30. 11. 2021 • 21:13

Teraz si limitu \(\lim_{n \to \infty } = \frac{6+\frac{7}{n}}{5+\frac{4}{n}}\)rozpíšeme na súčet dvoch limít v zmysle vety o súčte konvergentných postupnostiach. Dostaneme dve limity. Viete ich sem napísať? 

tyldonald 30. 11. 2021 • 20:49

Dobrý den,

mnohokrát děkuji za reakci. Děkuji také za odkaz ke konvergentním posloupnostem.

Možná jsem v předchozím příspěvku měl být trochu konkrétnější, za což se moc omlouvám, ale zhruba po tento krom kam jste mi to teď ukázal, tak jsem to z vašeho příspěvku již pochopil. Problém u mě nastává právě u použití těch vět.

A druhá věc ve které si právě nejsem jist, jak potom, když zjistím, že limita je skutečně těch 6/5, tak si nejsem úplně jist jak při důkazu dosadit do vzorce z definice.

Moc se omlouvám, že Vám to takhle komplikuji, ale nemám se koho jiného na tyto věci bohužel zeptat.

Ještě jednou moc děkuji za ochotu.

A.G. upraveno: 02. 12. 2021 • 08:48

Dobrý deň. Skúsim Vás na to naviesť, krok po kroku :)

1. Vieme, že \(\lim_{x \to \infty } \frac{1}{n} = 0\). Túto skutočnosť ľahko dokážeme priamym dôkazom. 
2. Vety pre súčet, rozdiel, súčin a podiel konvergentných postupností nájdete tu: https://isibalo.com/pdf/video/4bb8f534deea2c8ce400d329e9fadec5.pdf

Ako som už spomínal v predošlom príspevku, v čitateli i v menovateľi máme postupnosti, ktoré divergujú. To znamená, že majú nevlastnú limitu, konkrétne \(\infty \). 

Skúsme príklad zjednodušiť, majme zadanie:

\(\lim_{n \to \infty } = \frac{6n^{4}+7n^{3}}{5n^{4}+4n^{3}}\). Čitateľa i menovateľa výnasobíme výrazom \(\frac{1}{n^{4}}\). Dostaneme \(\lim_{n \to \infty } = \frac{6+\frac{7}{n}}{5+\frac{4}{n}}\). Výraz sme upravili tak, aby sme dostali konvergentné postupnosti. Práve teraz môžeme použiť vety vo výpise. 

Dokážete to vyriešiť ďalej sám?

tyldonald 29. 11. 2021 • 20:14

Dobrý den, moc děkuji za návod k tomuto příkladu. Napřed se moc omlouvám, že odepisuji skoro až po týdnu. Bohužel jsem trochu marodil.

Bohužel zatím ještě neznám větu o součtu konvergentních limit, takže ani nevím, jak do ní potom dosadit. Mohl bych vás poprosit, zda byste to ještě trochu podrobněji nerozepsal?

Předem moc děkuji za ochotu.