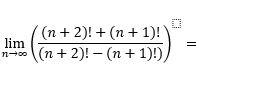Příklady od Vás: limita posloupnosti s faktoriály

Dominik Chládek 14. 11. 2020 • 17:28

Dobrý den,

takto:

\(\displaystyle \lim_{n\rightarrow\infty}\frac{(n+2)!+(n+1)!}{(n+2)!-(n+1)!}=\lim_{n\rightarrow\infty}\frac{(n+2)(n+1)!+(n+1)!}{(n+2)(n+1)!-(n+1)!}=\\\displaystyle =\lim_{n\rightarrow\infty}\frac{(n+1)!(n+2+1)}{(n+1)!(n+2-1)}=\lim_{n\rightarrow\infty}\frac{(n+2+1)}{(n+2-1)}=\lim_{n\rightarrow\infty}\frac{n+3}{n+1}=\\\displaystyle =\lim_{n\rightarrow\infty}\frac{n\left(1+{\displaystyle\frac3n}\right)}{n\left(1+{\displaystyle\frac1n}\right)}=\lim_{n\rightarrow\infty}\frac{1+{\displaystyle\frac3n}}{1+{\displaystyle\frac1n}}=\frac{1+0}{1+0}=1\)