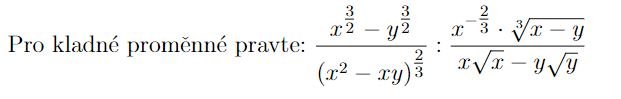Příklady od Vás:
úprava výrazu
Roman
18. 10. 2020 - 20:20
upraveno:
21. 10. 2020 - 18:55
Dobrý večer,
prosím o pomoc s řešením příkladu v příloze.
Děkuji, Roman
Dominik Chládek upraveno: 26. 10. 2020 • 09:40
Dobrý den, nějak takto:
\(\displaystyle\frac{x^{\frac32}-y^{\frac32}}{(x{(x-y))}^{\frac23}}\cdot\frac{x^\frac32-y^\frac32}{x^{-{\frac23}}{(x-y)}^{\frac13}}=\frac{\left(x^{\frac32}-y^{\frac32}\right)^2}{x{{}^{\frac23}(x-y)}^{\frac23}x^{-\frac23}{(x-y)}^\frac13}=\\\displaystyle=\frac{\left(x^{\frac32}-y^{\frac32}\right)^2}{x{{}^{\frac23-\frac23}(x-y)}^{\frac23+\frac13}}=\frac{\left(x^{\frac32}-y^{\frac32}\right)^2}{x^0{{}^{}(x-y)}^{\frac33}}=\frac{\left(x^{\frac32}-y^{\frac32}\right)^2}{(x-y)}\)
a to jde ještě rozkládat dál, ale zas tak velké zjednodušení to nebude :)
Dominik Chládek 26. 10. 2020 • 09:42
Dobrý den,
máte pravdu, byl to překlik a je to opraveno, moc Vám děkuji za upozornění! :)
Také na sebe dávejte pozor a přeji pevné zdraví! :)
Petr MRAK upraveno: 26. 10. 2020 • 03:05
Dobrý den řešiteli i žadateli o řešení,
velice názorný návod, jen ve jmenovateli předposledního výrazu má být zřejmě „x na nultou", (vytčeno před závorkou), aby ve finálním výrazu (výsledku) mohl ve jmenovateli zůstat pouze rozdíl (x – y) tak, jak uvedeno.
Pěkné dni přeje
Petr MRAK.
(Stay alive and safe)!
Dominik Chládek 21. 10. 2020 • 18:55
Není za co :)
Roman 20. 10. 2020 • 20:08
děkuji za vysvětlení, je to hezký příklad.