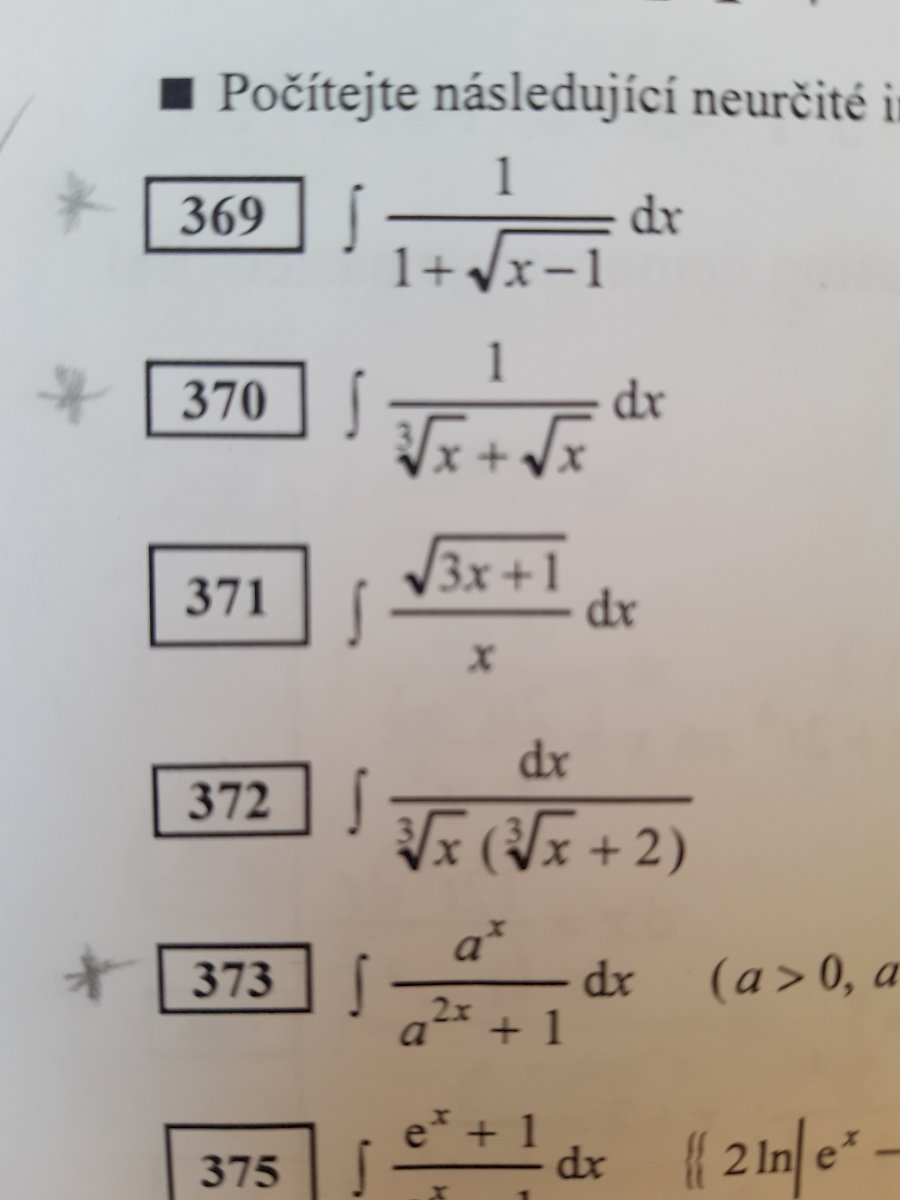Příklady od Vás:
Substituce integrálu
Nelča
09. 04. 2020 - 16:26
upraveno:
12. 04. 2020 - 18:46
Moc prosím o postup výpočtu u těchto 3 příkladů, 369,370 a 373, děkuji za vysvětlení !
Dominik Chládek 10. 04. 2020 • 12:52
Dobrý den,
369 - zde bych nejprve udělal substituci \(t^2=x-1\) a potom už to zvládnete v pohodě :)
370 - substitujte \(x=t^6\) a to vede na parciální zlomky :)
373 - díky tomu, že \(a^{2x}=(a^x)^2\) tak substitujte \(t=a^x\) a povede to na arcustangens :)
Dominik Chládek 11. 04. 2020 • 09:17
Takto:
\(\displaystyle\int2t\cdot\frac1{1+\sqrt{t^2}}dt=\int\frac{2t} {1+t}dt=\int\frac{2(1+t)-2}{1+t}dt=\\\displaystyle=\int\left(\frac{2(1+t)}{1+t}-\frac2{1+}dt=\right)dt=\int\left(2-\frac2{1+t}dt=\right)dt=\\=2t-\ln\left|1+t\right|=\;...\)
Nelča 10. 04. 2020 • 15:27
Vyjde mi to takto a ve výsledku se musí objevit minus, absolutně nevím, co s tím..
Nelča 10. 04. 2020 • 13:13
tu 369 počítám už třetí den a stále nechápu :D mám výsledek i půlku příkladu, ale nerozumím postupu