Příklady od Vás:
Aplikace, definice funkce
applosa1
20. 01. 2020 - 19:33
upraveno:
14. 05. 2020 - 11:44
Dobrý den, prosím o pomoc s touto úlohou.
Mějme obdelník, který má jeden vrchol na kladné poloose x, druhý na záporné poloose x a další dva vrcholy na křivce y= 16-ax^2, a>0 tak, aby y>0. Určete jeho rozměry tak, aby měl největší obvod v závislosti na parametru a. Určete tento obvod.
a další věcí s kterou si nevím rady je max a min v { } - jak mám tuto funkci definovat? nevím, jakým způsobem na to přijít :
když mám např. min {x^4-x^2; x^3-x}
Mám si to zadat jako x^4-x^2 <=x^3-x ?? a pak to počítat jako nerovnici
Předem moc děkuji za pomoc.
zdenek1 21. 01. 2020 • 09:02
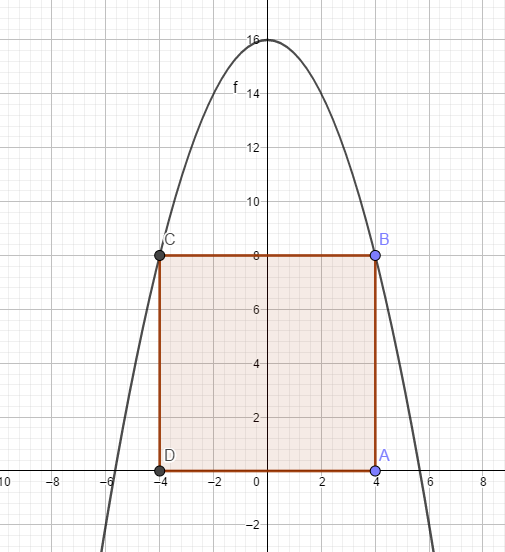
Když se podíváš na obrázek, uvidíš, jak přibližně to bude vypadat. Když bod A bude mít x-ovou souřadnici \(x\), vidíš, že obvod bude
\(o=4x+2(16-ax^2)=-2ax^2+4x+32\)
toto je kvadratická funkce, která má maximum ve vrcholu. x-ová souřadnice vrcholu je obecně \(x_v=\dfrac{-b}{2a} \), což v našem případě dává
\(x_v=\dfrac{-4}{2(-2a)}=\dfrac1a\)
Takže rozměry obdélníka budou: délka \(\dfrac2a\) a výška \(16-\dfrac1a\), maximální obvod pak \(o_{max}=32+\dfrac2a\)
ke druhé otázce: ano, řešíš nerovnci
