Příklady od Vás:
peiklad
Misa1987
19. 12. 2019 - 13:10
upraveno:
14. 05. 2020 - 11:44
muzete mi pomoct s prikladem: urcete polomer krivost a souradnice stredu oskulacni kruznice krivky k: y = e na -x v jejim pruseciku s osou y. udelala jsem prvni a druhou derivaci funkce (y) a pak dala do vzorce polomeru krivosti R = \( {[{1+(y')^2]} \over y''}\) a nevim jak dal. dekuji za pomoc
zdenek1 20. 01. 2020 • 13:02
Průsečík s osou y je \(T[0;1]\), derivace \(y^\prime=-e^{-x} \) a \(y^{\prime\prime}=e^{-x} \)
dosazením do vzorce: \(R=\dfrac{1+e^{2x}}{e^{-x}} \) a číselně pro \(x=0\) je \(R=2\)
Střed křivosti leží na normále v bodě dotyku, rovnice normály je obecně: \(y=y_0-\dfrac1{y_0^\prime}(x-x_0)\), kde \(T[x_0;y_0] \) je bod dotyku. Označíme střed \(S[m,n]\)
V našem případě pak máme \(n=1-\frac1{-1}(m-0)=m+1\)
Dále bod dotyku leží na kružnici se středem \(S\), poloměrem \(R\). Dosazením do rovnice kružnice dostaneme
\((0-m)^2+(1-n)^2=4 \) a dosadíme za \(n\)
\(m^2+(1-m-1)^2=4\ \Rightarrow\ m=\pm\sqrt2\). Z průběhu funkce pak vybereme kladný kořen.
Dostáváme \(S=[\sqrt2;\sqrt2+1] \)
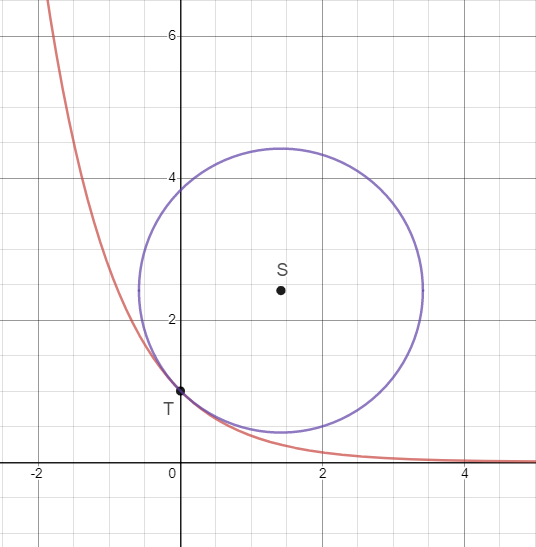
Celé to vidíme na obrázku
