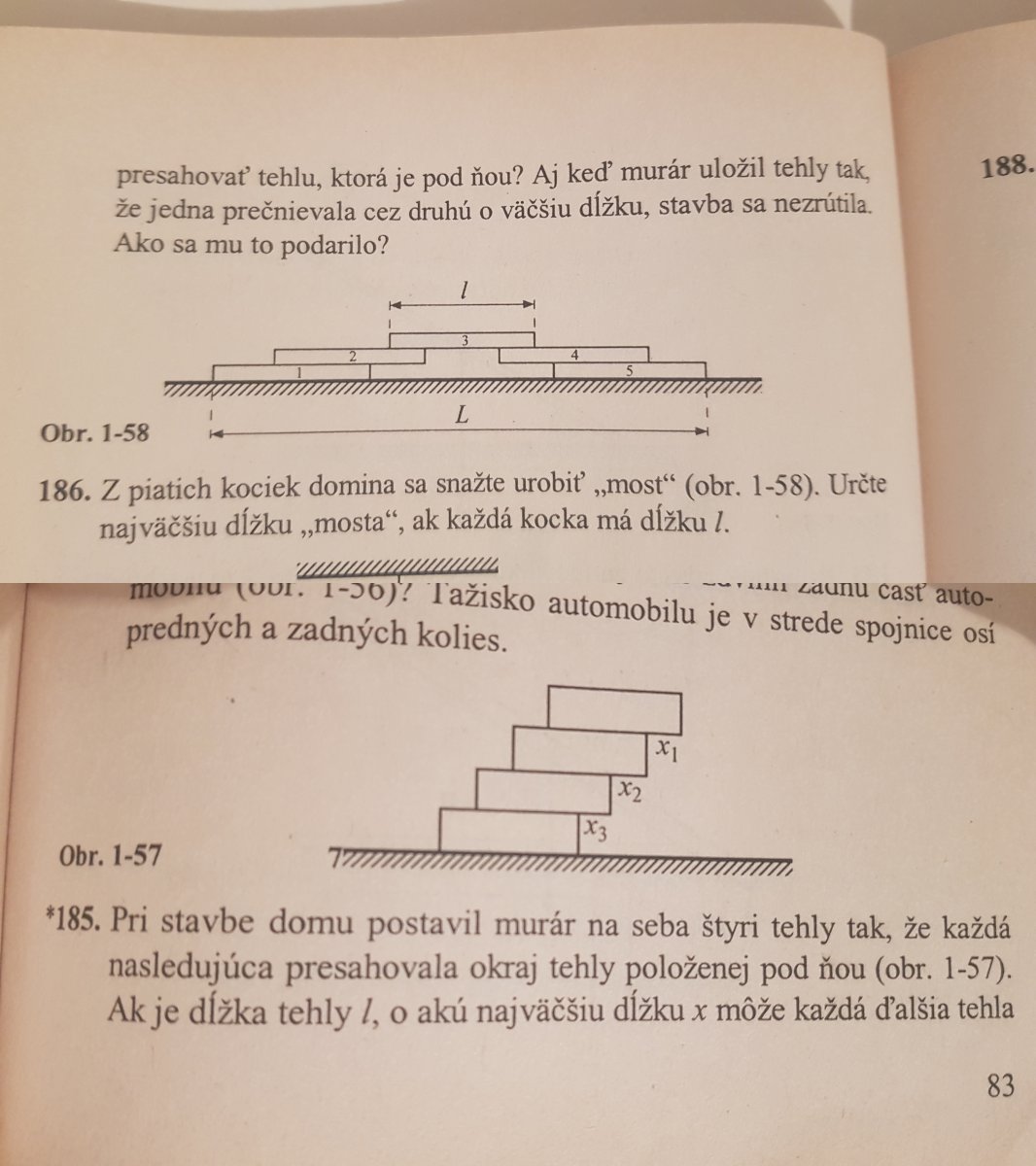
Příklady od Vás: Mechanika tuhého telesa - tehly

filda upraveno: 20. 02. 2019 • 23:54

Omlouvám se, ten závěr jsem přiliš nedomyslel :/
Nicméně správným řešením zdá se být toto:

Nejdříve rozeberme případ, kdy máme poze 3 cihly. Z výsledku výše víme, že nejvrchnější cihla (3) může tu pod ní (2) přečnívat maximálně o délku \(x_1 = l/2 \). Dále předpokládejme, že cihla (2) přečnívá nejspodnější cihlu (1) o délku \(x_2 \). Chceme tedy niní, aby hmotnost přečnívající části byla rozložena stejně jako "nepřečnívající" a to je splněno v krajním případě pro \(x_2 = l/4\) (pomůže nakreslit si obrázek). Přídáme nyní další cihlu (4), jež bude přečnívat o \(x_3\) a budeme opět hledat právě takové \(x_3\), kdy jsou přečnívající i nepřečnívající část symetrické, můžeme si tedy napsat rovnici:
\(x_3 + (x_2+x_3) + (x_1+x_2+x_3) = (l-x_3) + (l-x_2-x_3) + (l -x_1 - x_2 -x_3)\) a dosazením přislušných hodnot a vyřešením dostáváme \(x_3 = l/6\), celkově tedy nejvyšší cihla přečnívá nad nejspodnější o \(x = l/2 + l/4 +l/6 = \dfrac{11}{12}l\).

Zajimavé je "vykoukat" závislot pro n cihel, kdy \(x = \sum \limits_{k=1}^n \dfrac{l}{2k}\), pro \(n => \infty \), tato řada, ale diverguje, což znamená, že řada cihel může dosahovat libovolně daleko :)

186) více méně ty samé úvahy :) 

filda 17. 02. 2019 • 21:59

185) Nejprve bych se podíval na případ, kdy máme pouze 2 cihly a chceme zjistit o jakou max. délku \(x \) může vrchní cihla přečnívat přes tu spodní. Aby se těleso nacházelo ve statické poloze musí být výslednice momentů sil působící na těleso nulová \(\sum \limits_a \vec{M}^a = 0 \) a \(\vec{M} = \vec{r} \times \vec{F}\) pro velikost \(M = rFsin\varphi = Fs\) kde \(s\) je rameno síly. Dále volme počátek souřadné soustavy v levém dolním rohu spodní cihly a hmotnost jedné cihly \(m_0\) . Vrchní cihlu si rozdělme na část, jež přečnívá a nepřečnívá o hmotnostech \(m_1\) a \(m_2\) , kdy \(m_0 = m_1 + m_2 \). Obě tyto části budou mít ze symetrie tělesa těžiště ve své polovině. Osa otáčení bude právě pravý hroní roch spodní cihly. A pak tedy zjevně:

\(m_1g\dfrac{l-x}{2} = m_2 g \dfrac{x}{2}\), ještě potřebujeme vyjádřit závislost \(m_1, m_2\) na \(x\) , tato závsilost bude lineární (přímo úměrné s x klesá/roste \(m_1 / m_2 \)) a tedy:

\(\left( m_0 - \dfrac{m_0}{l}x \right)\dfrac{l-x}{2} = \dfrac{m_0}{l}x \dfrac{x}{2} => x=\dfrac{l}{2}\) 

Což ale odpovídá celkovému těžišti vrchní cihly přimo nad osou otáčení.

Máme-li takto 3 přečnívající cihly, musí opět jejich výsledné těžiště být přímo nad osou otáčení, což je ekvivalentní s tím, že max polovina hmotnosti cihel může přečnívat a tedy se nabízí varianta, že cihly přes sebe přčnívají o \(x = l/6\) .

186) obdobná úvaha, tíha nejvrchnější cihly se rozdělí mezi oba "podstavce" rovnoměrně + podmíky a úvahy výše. Já dospěl k hodnotě\(L = 3l \)