Složitější logaritmické rovnice
Řešená cvičení
Logaritmické rovnice
Střední škola • 3 min
Vyřešte následující logaritmickou rovnici v oboru reálných čísel \(\mathbb{R}\):
\(\dfrac{\log x+1}{2+ \log x}+\dfrac{2\log x-1}{\log x}\) \(=3\)
Logaritmické rovnice
Střední škola • 7 min
Vyřešte následující logaritmickou rovnici v oboru reálných čísel \(\mathbb{R}\):
\(\log_4^2 x^3-\dfrac{4}{\log_4^2 x^2}\) \(=8\)
Logaritmická rovnice
Střední škola • 3 min
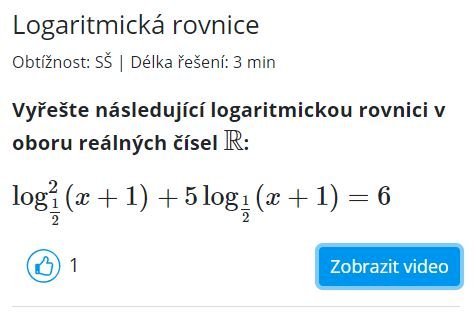
Vyřešte následující logaritmickou rovnici v oboru reálných čísel \(\mathbb{R}\):
\(\log_\frac12^2(x+1)\;+\) \(5\log_\frac12(x+1) =6\)
Testy
-%
Zhlédnutí videa
Střední škola • 1 min
-%
Potvrzení -%
Podrobnosti o látce
Autor videa
Dominik Chládek
Autor matematiky na isibalu :)
Klíčová slova
Střední škola
Odhadovaná délka studia
0 h 26 min
Komentáře
brezover 31. 12. 2020 • 23:37
Asi jsem si něčeho nevšimla, ale nezdá se mi to řešení u 3. řešeného příkladu, podle mě je řešením jen 63. Mohu poprosit o kontrolu? Případně vysvětlení? Nezdá se mi, že by mohlo být x záporné.
Dominik Chládek 01. 01. 2021 • 20:16
Dobrý den,
zkuste si dosadit do toho logaritmu, uvidíte, že vnitřek vyjde kladný i přes to, že dosazujete záporné číslo :)
radovan.skvor 20. 02. 2018 • 15:31
Tenhle vzoreček je dobrej pro hloupjejší kalkulačky co neuměj počítat jiný nez dekadický logaritmus
Dominik Chládek 30. 09. 2017 • 18:00
Existuje, je to tento vzorec:
\(\log_ax=\dfrac{\log_b x}{\log_b a}\)
tak s ním můžete měnit logaritmy o různých základech :)
erorrek 30. 09. 2017 • 14:27
Myslel jsem spíš obecně, zda existuje něaký způsob jak je převést na logaritmus o stejném základu)
Dominik Chládek 30. 09. 2017 • 10:03
Dobrý den, to vůbec nevadí, jsem rád za zpětnou vazbu, jasně že to neotravuje :) no to pak záleží příklad o příkladu, máte nějaký konkrétní na mysli?
erorrek 29. 09. 2017 • 22:57
Začíná se mi zdát, že jsem tu nejaktivnější komentátor :D. Snad vás to moc neotravuje.
Zajímalo by mě co dělat, když máme více logaritmů o různém základu?