Reimann Bernard

Předpoklady NESPLNĚNY

Vědecké objevy, a zvláště ty matematické, významně závisejí na území, které je zkoumáno, a na vědomostech do té doby získaných. Když se mezi čísly pouze procházíte, je důležité neztratit správný směr, když ale po nich stoupáte vzhůru, je to docela jiná záležitost. Dříve nebo později dojdete do výšky, kdy už musíte mít jistou horolezeckou průpravu a řádné vybavení, abyste mohli pokračovat. Vylézt do 4 000 metrů je něco úplně jiného než vystoupat do 2 000 metrů. Procházka s Riemannem patří zcela jistě do kategorii horolezení „4 000 metrů a výše“.

Georg Fridrich Bernard Riemann se narodil 17. 9. 1826 v Breselenzu v Německu do rodiny chudého luteránského pastora. Otec se věnoval výuce všech svých šesti dětí a vyučoval plachého, introvertního, ale velmi nadaného Bernarda až do jeho deseti let, kdy mu se vzděláním začal pomáhat učitel místní školy. Ve čtrnácti letech vstoupil přímo do třetího ročníku Licea v Hannoveru, od roku 1842 pokračoval na Gymnázium v Lüneburgu. Zdá se, že byl dobrým, nikoli však výborným studentem. Zvláštní zájem projevoval o matematiku. Ředitel gymnázia si všiml Riemannova nadání a umožnil mu studium matematických textů z jeho osobní knihovny. Zapůjčil mu i osmisetstránkovou Teorii čísel Adriena Legendra. Když se ho po šesti dnech zeptal, kam až se dostal, odpověděl Riemann: „Je to opravdu báječná kniha, zvládl jsem ji". Uplynulo několik let a Riemann vytvořil vlastní teorii prvočísel, v níž využil znalosti získané z Legendreovy knihy a vytvořil jednu z nejslavnějších hypotéz v dějinách matematiky.

Na otcovo přání odešel studovat do Göttingen filozofii a teologii, zapsal si i přednášky z matematiky u Karla Gausse. Po roce přešel do Berlína k Peteru Dirichletovi, Carlu Jocobimu a Ferdinandu Eisensteinovi, ale studia dokončil opět v Göttingenu, kde po dokončení studia zůstal.

Rodiče mu předčasně zemřeli na tuberkulózu a na tuto nemoc postupně umírali i jeho sourozenci. Mladý Riemann tušil, že takový bude velmi pravděpodobně i jeho osud. Cesty ze školy pěšky domů, kterých se nechtěl vzdát, ho unavovaly a byly doprovázeny prvními zdravotními obtížemi. Osud mu dopřál jen 15 let práce.

Své myšlenky vyložil v roce 1854 konkurzní přednášce, kterou pronesl v sále göttingenské univerzity. Až dosud se neeuklidovská geometrie zabývala jen zakřivenou dvourozměrnou plochou. Riemann ukázal, že stejným způsobem lze studovat zakřivené prostory o jakémkoliv počtu rozměrů. Riemannova teorie byla nesmírně široká a komplexní. Všechny dosavadní geometrie, byly jen dílčími případy Riemannovy geometrie. V jeho teorii mohl být prostor nejrůznějším způsobem zkroucený, zdeformovaný, mohl mít různou křivost v různých bodech, mohl být souvislý i děravý, mohl mít libovolný počet rozměrů. Říká se, že když stárnoucí „král matematiků“ Gauss přednášku svého bývalého žáka vyslechl, jen mlčky vstal a beze slova vyšel ze sálu. K tomu, co Bernard Riemann dokázal, nebylo už co dodat.

Riemannův vliv byl zpočátku menší než by mohl být. Göttingen byla malá univerzita, situaci zhoršil i fakt, že někteří jeho nejlepší studenti zemřeli velmi mladí. Jeho práce si však postupně získala respekt významných německých matematiků. V roce 1859 byl Riemann jmenován na göttingenské univerzitě profesorem. O tři roky později se oženil a dočkal se narození dítěte, mnoho času na rodinné radosti mu už ale nezbývalo. Kvůli zhoršujícímu se zdraví pobýval hlavně ve slunné Itálii. Riemann se ještě jednou nakrátko vrátil do Göttingenu a potom se vydal zpět do Itálie. Mezitím vypukla prusko-rakouská válka a železnice nefungovala. Riemann šel pěšky, ale cesta byla vyčerpávající a na kraji Itálie v nedožitých čtyřiceti letech zemřel.

Z malé univerzity v Güttingenu se později stalo světové centrum matematického výzkumu s Carlem Gaussem a Bernardem Riemannem jeho ikonickými osobnostmi.

*****

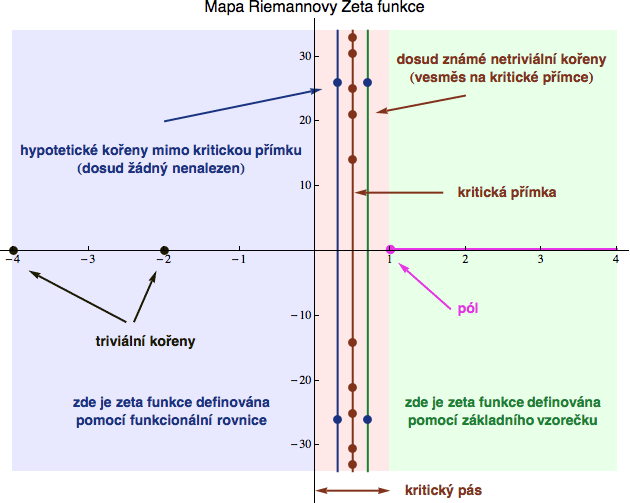
Riemannova hypotéza „Reálná část netriviálního nulového bodu zeta funkce je rovna 1/2.“
https://youtu.be/sD0NjbwqlYw

Riemann se pustil do jejich studia a všiml si, že prvních pár netriviálních kořenů se nalézá na přímce x=1/2, vyslovil proto domněnku, že všechny ostatní (netriviální) kořeny zeta funkce leží na kritické přímce, ale přiznal, že to neumí dokázat. Zatím zde leží všechny známé netriviální kořeny. Riemannova hypotéza tvrdí, že na přímce 1/2 leží všechny netriviální nuly. Stačilo by najít jediný takový kořen, který leží jinde, a hypotéza by přestala platit. Známe už miliardy netriviálních kořenů a všechny leží na přímce 1/2. Pokud tedy zanalyzujete všechna řešení rovnice Zeta(z)=0 v komplexní rovině, pak stačí, když ukážete, že všechny netriviální kořeny leží v komplexní rovině na vertikální přímce x = ½, Clayův matematický institut Vám vyplatí jeden milion dolarů, nezávisle na věku, pohlaví a zaměstnání

Pokud je tato hypotéza správná, jsou prvočísla rozložena pravidelně – či spíše tak pravidelně, jak je to jen možné. Abychom si to přiblížili, použijeme analogii. Představme si funkci, která představuje rozklad zvukových vln, řadu sinusovek, z nichž se skládá třeba zvuk houslí. Pro jednoduchost předpokládejme, že hrají jen jedny housle. Zároveň s dobře zřetelnými maximy a minimy křivky jsou vidět i drobné nepravidelné odchylky, které narušují harmonický průběh grafu. V žargonu akustiky se jím říká „bílý šum“ a má různé příčiny: atmosférické poruchy, šum pozadí a podobně. Riemannova hypotéza říká, že nepravidelnost v rozdělení prvočísel je způsobena matematickým „bílým šumem“, což znamená, že rozložení prvočísel sleduje určitou zákonitost a není čistě náhodné. V tomto smyslu se Riemannovi podařilo vnést jistý řád do nesourodého světa prvočísel.

Vynikajícího německého matematika Davida Hilberta se jednou dotázali,na kterou věc by se zeptal na matematickém sympoziu konaném 100 let po jeho smrti. „Zeptal bych se, jestli už byla dokázána Riemannova hypotéza,“zněla odpověď. Dodneška nikdo s důkazem nepřišel, máme ovšem ještě čas, Hilbert zemřel v roce 1943.

 

 

Návaznosti